What Is 40 Of 4000
wordexpert
Sep 24, 2025 · 5 min read
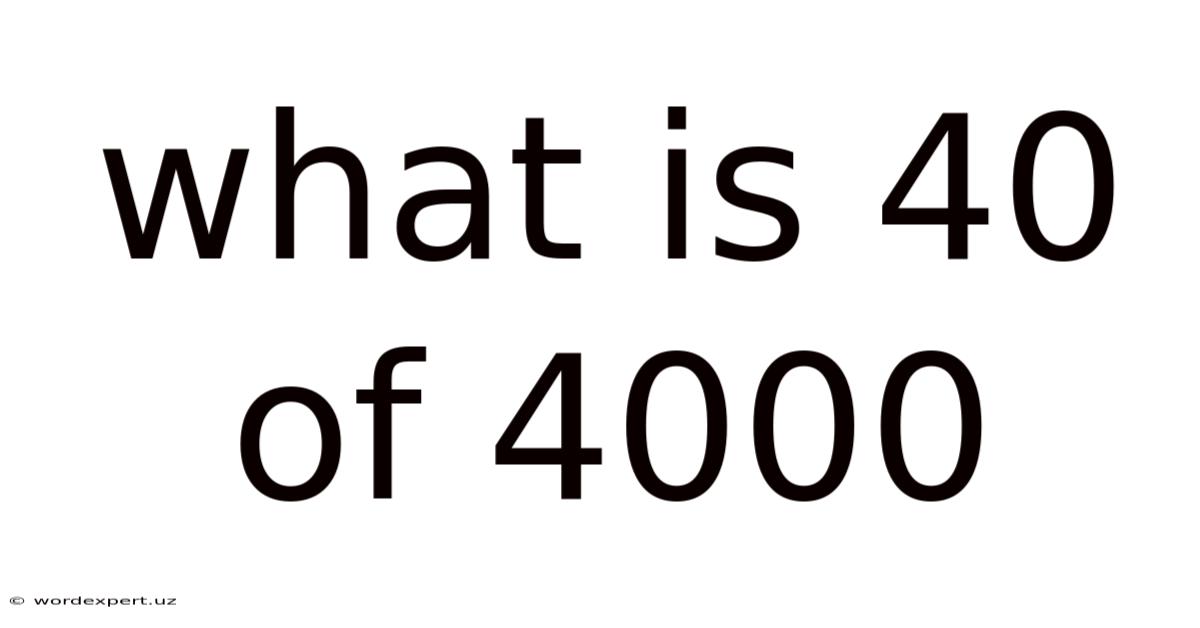
Table of Contents
What is 40 of 4000? Understanding Percentages and Proportions
Finding out "what is 40 of 4000?" might seem like a simple arithmetic problem, but it opens the door to understanding fundamental concepts in mathematics, crucial for various applications in everyday life and advanced studies. This article will delve into calculating this specific value, exploring the underlying principles of percentages and proportions, and demonstrating its practical relevance. We'll cover different calculation methods, explain the significance of such calculations, and answer frequently asked questions to solidify your understanding.
Understanding the Problem: 40 out of 4000
The question "What is 40 of 4000?" essentially asks us to determine the proportional relationship between the number 40 and the number 4000. This relationship can be expressed in several ways: as a fraction, a decimal, or a percentage. Each representation offers a unique perspective on the relative size of 40 compared to 4000. This seemingly simple question underlies many real-world scenarios, from calculating discounts and tax rates to analyzing statistical data and determining probabilities.
Method 1: Calculating the Fraction
The most direct approach is to express the relationship as a fraction. We can represent "40 of 4000" as the fraction 40/4000. This fraction can then be simplified by dividing both the numerator (40) and the denominator (4000) by their greatest common divisor (GCD), which is 40.
40/4000 = (40 ÷ 40) / (4000 ÷ 40) = 1/100
This simplified fraction, 1/100, clearly shows that 40 represents one-hundredth of 4000.
Method 2: Converting the Fraction to a Decimal
To express the relationship as a decimal, we simply divide the numerator of the simplified fraction by the denominator:
1 ÷ 100 = 0.01
Therefore, 40 represents 0.01 (one hundredth) of 4000.
Method 3: Calculating the Percentage
A percentage is simply a fraction expressed as parts per hundred. Since we've already established that 40 is 1/100 of 4000, we can easily convert this fraction to a percentage:
(1/100) * 100% = 1%
Thus, 40 is 1% of 4000. This percentage representation provides a readily understandable and commonly used way to express the proportional relationship between the two numbers.
Method 4: Using Proportions
Proportions offer a more formal mathematical approach to solving this type of problem. A proportion states that two ratios are equal. We can set up a proportion to solve for the percentage:
x/100 = 40/4000
where 'x' represents the percentage we want to find. To solve for x, we can cross-multiply:
4000x = 4000
x = 4000/4000 = 1
Therefore, x = 1%, confirming our previous result. This method is particularly useful when dealing with more complex proportional relationships.
The Significance of Percentage Calculations
The ability to calculate percentages is a fundamental skill with wide-ranging applications:
-
Financial Calculations: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentages is essential for making informed financial decisions.
-
Statistical Analysis: Percentages are used extensively in statistical analysis to represent proportions within data sets. This allows for easy comparison and interpretation of trends and patterns. For instance, understanding the percentage of a population that holds a particular opinion is crucial for market research or political polling.
-
Scientific Research: In scientific studies, percentages are used to express the relative abundance of certain elements or compounds, the success rate of experiments, or the prevalence of a particular disease.
-
Everyday Life: From calculating tips at restaurants to understanding sale prices in stores, percentages are ubiquitous in our daily lives. The ability to quickly and accurately calculate percentages improves efficiency and decision-making.
-
Data Representation: Percentages provide a standardized way to compare different datasets, even if those datasets are of vastly different sizes. This makes comparing results and drawing conclusions easier.
Practical Examples of Percentage Calculations
Let's consider a few real-world scenarios where understanding "40 of 4000" – or similar percentage calculations – is vital:
-
Inventory Management: A warehouse contains 4000 units of a particular product. If 40 units are damaged, what percentage of the inventory is damaged? (Answer: 1%) This information helps businesses assess losses and manage inventory effectively.
-
Quality Control: In a manufacturing process, 4000 items are produced. 40 items fail quality control. What percentage of the production run is defective? (Answer: 1%) This helps identify areas needing improvement in the production process.
-
Survey Results: A survey is conducted with 4000 respondents. 40 respondents choose a particular option. What percentage of respondents chose that option? (Answer: 1%) This is crucial for interpreting survey data and drawing meaningful conclusions.
Frequently Asked Questions (FAQ)
Q1: How can I calculate percentages quickly without a calculator?
A1: For simple percentages like 10%, 25%, or 50%, you can often perform mental calculations. For example, 10% is simply dividing by 10, 25% is dividing by 4 and multiplying by 1, and 50% is dividing by 2. For other percentages, you can break them down into simpler fractions (e.g., 15% = 10% + 5%).
Q2: What if the numbers aren't as easily divisible?
A2: For more complex calculations, using a calculator or spreadsheet software is recommended for accuracy. The proportion method described earlier provides a systematic approach for solving any percentage problem regardless of the numbers involved.
Q3: Are there any online tools to help calculate percentages?
A3: Yes, many online calculators and websites offer percentage calculation tools. These can be particularly helpful for quick calculations or for checking your work. However, understanding the underlying principles is crucial for solving problems effectively.
Q4: Why is understanding percentages important in higher-level mathematics?
A4: Percentages and proportional reasoning form the foundation for more advanced mathematical concepts, including probability, statistics, calculus, and financial modeling. A solid grasp of percentage calculations is essential for success in these areas.
Conclusion
Determining "what is 40 of 4000" involves understanding the fundamental concepts of fractions, decimals, and percentages. We've explored different methods to solve this problem, demonstrating its practical applications in various fields, from finance and statistics to everyday life. The ability to calculate percentages accurately and efficiently is a crucial skill with far-reaching implications, enabling informed decision-making and a deeper understanding of quantitative data. Mastering this seemingly simple calculation unlocks a gateway to a more comprehensive understanding of the world around us, expressed in numbers and proportions.
Latest Posts
Latest Posts
-
17 Gallons How Many Quarts
Sep 24, 2025
-
How Many Mg In Pound
Sep 24, 2025
-
Angle Of Impact Blood Spatter
Sep 24, 2025
-
25 Fl Oz To Ml
Sep 24, 2025
-
Area Of Piecewise Rectangular Figure
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 4000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.