What Is 5 Of 15
wordexpert
Sep 12, 2025 · 6 min read
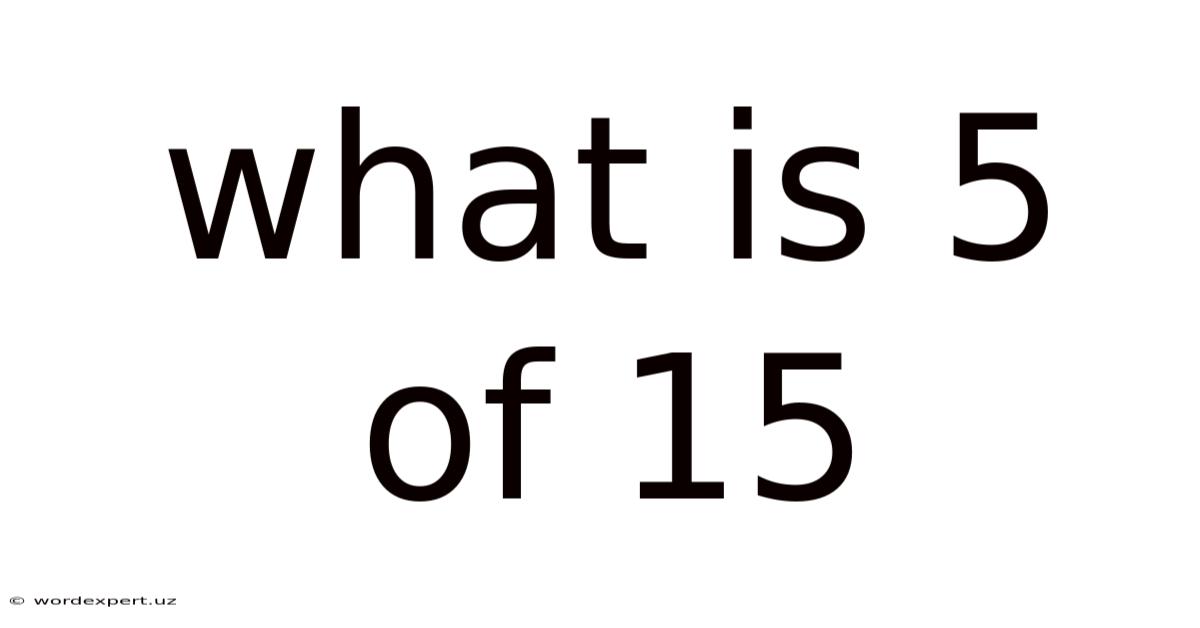
Table of Contents
What is 5 of 15? Understanding Fractions, Ratios, and Percentages
The seemingly simple question, "What is 5 of 15?", opens a door to a world of mathematical concepts vital for everyday life. It's more than just a basic arithmetic problem; it's a gateway to understanding fractions, ratios, and percentages – tools we use to compare quantities, express proportions, and make calculations in various fields from cooking and finance to science and engineering. This article will explore this question comprehensively, breaking down the different ways to interpret and solve it, and expanding on the underlying mathematical principles.
Understanding the Question: Different Interpretations
The phrase "5 of 15" can be interpreted in several ways, depending on the context. Each interpretation leads to a different mathematical operation and a different answer, highlighting the importance of clear communication in mathematical problems.
-
Part of a Whole (Fraction): This is the most common interpretation. "5 of 15" means 5 out of a total of 15. This translates directly into a fraction: 5/15.
-
Ratio: "5 of 15" can also represent a ratio, comparing the quantity 5 to the quantity 15. This ratio can be written as 5:15.
-
Percentage: We can express "5 of 15" as a percentage, representing the proportion of 5 relative to 15 as a fraction of 100.
Calculating the Fraction: 5/15
The fraction 5/15 represents the proportion of 5 out of 15. To simplify this fraction, we find the greatest common divisor (GCD) of the numerator (5) and the denominator (15). The GCD of 5 and 15 is 5. Dividing both the numerator and denominator by 5, we get:
5 ÷ 5 / 15 ÷ 5 = 1/3
Therefore, 5 of 15 is equivalent to 1/3. This means that 5 represents one-third of the total quantity of 15.
Understanding Ratios: 5:15
A ratio is a comparison of two or more quantities. The ratio 5:15 compares the quantity 5 to the quantity 15. Just like fractions, ratios can be simplified by dividing both parts by their greatest common divisor. In this case, the GCD is again 5:
5 ÷ 5 : 15 ÷ 5 = 1:3
The simplified ratio 1:3 indicates that for every one unit of the first quantity, there are three units of the second quantity. This ratio is equivalent to the fraction 1/3.
Expressing as a Percentage: Converting 1/3 to Percentage
To express the fraction 1/3 as a percentage, we need to convert it to a fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by a number that results in a denominator of 100. However, since 3 doesn't divide evenly into 100, we'll use decimal representation:
1/3 ≈ 0.3333...
To convert the decimal to a percentage, we multiply by 100:
0.3333... × 100 ≈ 33.33%
Therefore, 5 of 15 is approximately 33.33%. The "..." indicates that the decimal representation of 1/3 is a repeating decimal, extending infinitely. In practical applications, we often round to a suitable number of decimal places.
Real-World Applications: Illustrative Examples
Understanding fractions, ratios, and percentages is crucial in many real-world scenarios. Here are a few examples showcasing how the concept of "5 of 15" applies:
-
Baking: If a recipe calls for 15 tablespoons of flour, and you only want to make one-third of the recipe, you would use 5 tablespoons (5/15 = 1/3).
-
Sales: If a store has 15 items of a particular product and 5 are sold, the fraction of items sold is 5/15 or 1/3 (33.33%).
-
Surveys: If 15 people were surveyed and 5 responded positively to a question, the positive response rate is 5/15 or 1/3 (33.33%).
-
Gardening: If you have 15 plants and 5 of them are diseased, the proportion of diseased plants is 5/15 or 1/3 (33.33%).
-
Finance: If you invest $15,000 and earn $5,000 in profit, your profit represents 5/15 or 1/3 (33.33%) of your investment.
Further Exploring Fractions, Ratios, and Percentages
The concept of "5 of 15" provides a foundational understanding of several key mathematical concepts. Let's delve deeper into each of these:
Fractions:
-
Numerator and Denominator: A fraction consists of a numerator (the top number) and a denominator (the bottom number). The numerator represents the part, and the denominator represents the whole.
-
Simplifying Fractions: Simplifying fractions involves reducing them to their lowest terms by dividing both the numerator and the denominator by their greatest common divisor.
-
Equivalent Fractions: Different fractions can represent the same proportion. For example, 1/3, 2/6, and 3/9 are all equivalent fractions.
-
Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to the denominator (e.g., 5/3). A mixed number combines a whole number and a fraction (e.g., 1 2/3).
Ratios:
-
Writing Ratios: Ratios can be written in several ways: using a colon (e.g., 5:15), using the word "to" (e.g., 5 to 15), or as a fraction (e.g., 5/15).
-
Simplifying Ratios: Like fractions, ratios can be simplified by dividing both parts by their greatest common divisor.
-
Proportions: A proportion is a statement that two ratios are equal. Proportions are used to solve many practical problems involving scaling and similar shapes.
Percentages:
-
Converting Fractions and Decimals to Percentages: To convert a fraction or decimal to a percentage, multiply by 100 and add the "%" symbol.
-
Converting Percentages to Fractions and Decimals: To convert a percentage to a fraction or decimal, divide by 100 and remove the "%" symbol.
-
Percentage Increase and Decrease: Percentage increase and decrease are used to express changes in quantities as a percentage of the original value.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of the fraction 5/15?
A1: The simplest form of 5/15 is 1/3.
Q2: Can ratios be expressed as decimals or percentages?
A2: Yes, ratios can be expressed as decimals or percentages by dividing the first term by the second term and then multiplying by 100 for percentages.
Q3: How do I calculate a percentage of a number?
A3: To calculate a percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, 33.33% of 100 is 100 × 0.3333 ≈ 33.33.
Q4: What if the numbers weren't 5 and 15? How would I approach a similar problem?
A4: The same principles apply. For example, if the question was "What is 7 out of 21?", you would form the fraction 7/21, simplify it (to 1/3), and then convert it to a decimal (0.3333...) and a percentage (33.33%).
Conclusion
The seemingly simple question, "What is 5 of 15?", serves as a powerful illustration of fundamental mathematical concepts. By understanding fractions, ratios, and percentages, and the relationships between them, we equip ourselves with essential tools for problem-solving in a wide range of everyday situations. This knowledge extends far beyond simple arithmetic, laying the groundwork for more advanced mathematical concepts and applications in various disciplines. Mastering these concepts empowers us to analyze data, interpret proportions, and make informed decisions in various aspects of our lives.
Latest Posts
Latest Posts
-
6 Grams Yeast To Tsp
Sep 12, 2025
-
Calculate Area Of Irregular Triangle
Sep 12, 2025
-
How Long Is 6000 Hours
Sep 12, 2025
-
How Many Hours Till 5
Sep 12, 2025
-
How To Do Square Yards
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.