What Is 50 Of 12
wordexpert
Sep 17, 2025 · 5 min read
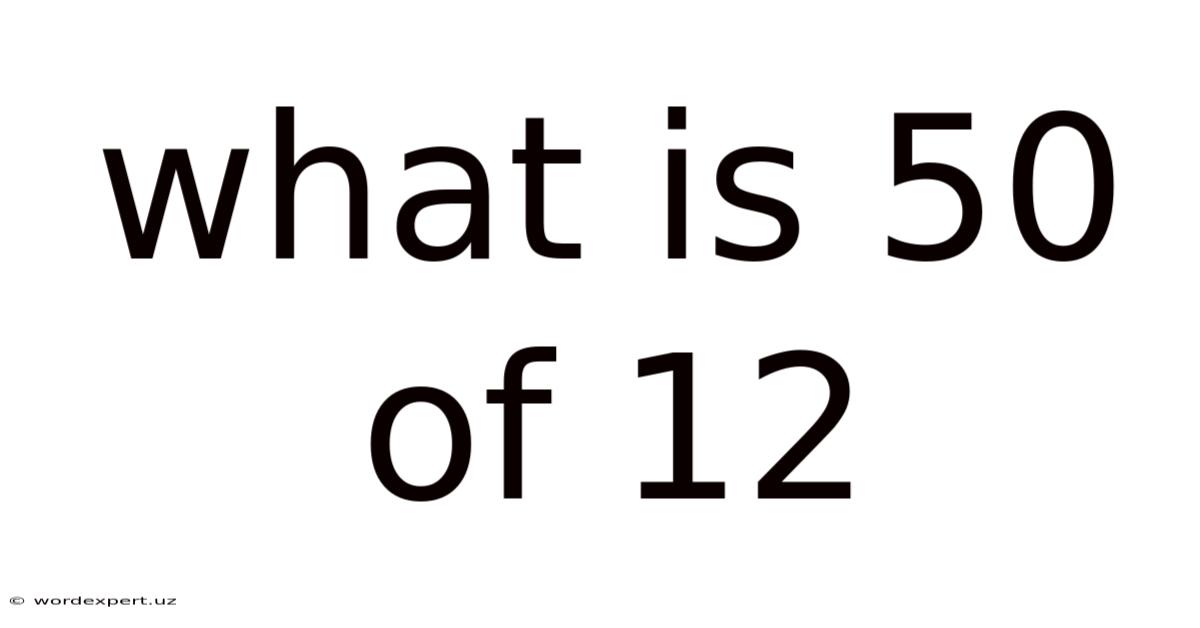
Table of Contents
What is 50% of 12? A Deep Dive into Percentages and Their Applications
Finding 50% of 12 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to calculate percentages, particularly this seemingly basic example, forms the foundation for a wide range of applications in everyday life, from calculating discounts and sales tax to understanding financial statements and interpreting statistical data. This article will not only answer the question "What is 50% of 12?" but also delve into the underlying concepts, providing a comprehensive understanding of percentages and their practical uses.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal. Understanding this fundamental equivalence is crucial for solving percentage problems.
Calculating 50% of 12: The Simple Approach
The simplest way to calculate 50% of 12 is to remember that 50% is equivalent to one-half (1/2). Therefore, finding 50% of 12 is the same as finding half of 12. This is a simple division problem:
12 / 2 = 6
Therefore, 50% of 12 is 6.
Calculating 50% of 12: The General Percentage Formula
While the above method works perfectly for 50%, it's beneficial to understand the general formula for calculating percentages, which is applicable to any percentage and any number. The formula is:
Percentage × Number = Result
Or, more formally:
(Percentage/100) × Number = Result
Applying this formula to our problem:
(50/100) × 12 = 0.5 × 12 = 6
This confirms our earlier answer. This formula is versatile and can be used to calculate any percentage of any number.
Beyond the Basics: Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios. Let's explore some examples:
-
Sales and Discounts: Stores frequently advertise sales with percentage discounts. For instance, a 25% discount on a $40 item can be calculated using the formula: (25/100) × $40 = $10. The final price would be $40 - $10 = $30.
-
Taxes: Sales tax is usually expressed as a percentage of the purchase price. If the sales tax is 8% and you buy an item for $100, the tax amount is (8/100) × $100 = $8. The total cost would be $100 + $8 = $108.
-
Tips and Gratuities: When dining out, it's customary to leave a tip, often expressed as a percentage of the bill. Calculating a 15% tip on a $50 meal involves calculating (15/100) × $50 = $7.50.
-
Interest Rates: Interest rates on loans and savings accounts are expressed as percentages. Understanding percentage calculations allows you to accurately determine the interest earned or paid over a specific period.
-
Financial Statements: Financial reports like balance sheets and income statements utilize percentages extensively to show ratios and proportions of different financial components. For example, profit margins are often expressed as a percentage of revenue.
-
Statistics and Data Analysis: Percentages are used extensively in statistics to represent proportions within a data set. For example, survey results might indicate that 60% of respondents preferred a particular product.
Working with Different Percentages: Strategies and Tips
While calculating 50% is straightforward, calculating other percentages might require a slightly different approach. Here are some helpful strategies:
- Using Fractions: Many percentages have simple fractional equivalents. For example:
- 25% = 1/4
- 75% = 3/4
- 10% = 1/10
- 20% = 1/5
Using these equivalents can often simplify calculations. For example, finding 25% of 20 is the same as finding 1/4 of 20, which is 20/4 = 5.
-
Breaking Down Percentages: Complex percentages can be broken down into simpler parts. For instance, to calculate 35% of a number, you can calculate 30% and 5% separately and add the results.
-
Using a Calculator: For more complex percentage calculations, a calculator is a valuable tool. Most calculators have a percentage function (%) that simplifies the process.
-
Working Backwards: If you know the result and the percentage, you can calculate the original number. For example, if 20% of a number is 10, the original number is 10/(20/100) = 50.
Common Mistakes to Avoid When Calculating Percentages
-
Confusing Percentage with Decimal: Remember to divide the percentage by 100 before multiplying by the number. Failing to do so will lead to incorrect results.
-
Incorrect Order of Operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with money. It's often best to use the full decimal value in calculations and round only at the final stage.
Frequently Asked Questions (FAQ)
-
What is the easiest way to calculate percentages? The easiest way depends on the specific percentage. For simple percentages like 50%, 25%, or 10%, using fractional equivalents is often quickest. For other percentages, the general formula [(Percentage/100) × Number] or a calculator is recommended.
-
How do I calculate a percentage increase or decrease? To calculate a percentage increase, find the difference between the new value and the original value, divide this difference by the original value, and multiply by 100. A percentage decrease is calculated similarly.
-
How can I improve my percentage calculation skills? Practice is key! Try solving various percentage problems with different numbers and percentages. Start with simple problems and gradually move to more complex ones.
-
Are there any online tools or calculators that can help me with percentage calculations? Yes, numerous websites and apps offer percentage calculators that can perform complex percentage calculations quickly and accurately.
Conclusion: Mastering Percentages – A Lifelong Skill
The seemingly simple question, "What is 50% of 12?" opens the door to a much broader understanding of percentages and their vital role in everyday life. From managing personal finances to analyzing data, proficiency in percentage calculations is a valuable and versatile skill. By understanding the underlying concepts and practicing different calculation methods, you can confidently tackle any percentage-related problem and confidently navigate the numerical world around you. Remember that consistent practice is the key to mastering this essential mathematical concept. Don't be afraid to explore different approaches and utilize available resources to enhance your understanding and speed in calculating percentages.
Latest Posts
Latest Posts
-
How Long Is 69 Weeks
Sep 17, 2025
-
How Much Is 3000 Pennies
Sep 17, 2025
-
How Much Longer Until 2
Sep 17, 2025
-
How Many Nickels In 1
Sep 17, 2025
-
How Long Is 65 Days
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.