What Is 6 Of 250
wordexpert
Sep 17, 2025 · 5 min read
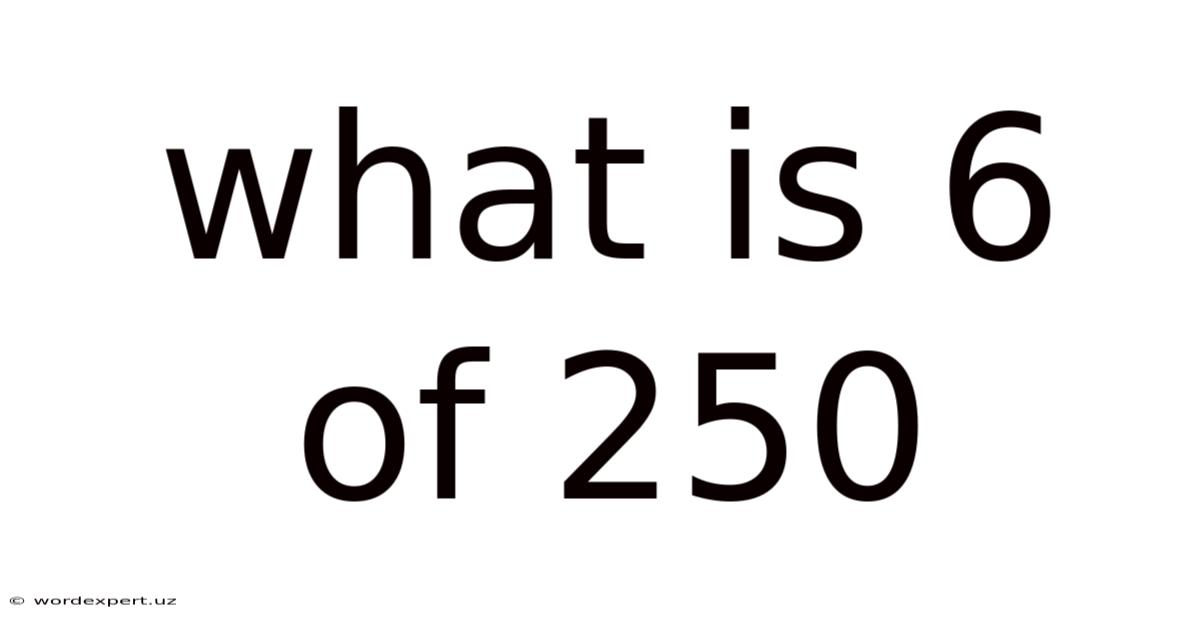
Table of Contents
What is 6 of 250? Understanding Fractions, Percentages, and Ratios
This article explores the question "What is 6 of 250?" It goes beyond a simple numerical answer, delving into the underlying mathematical concepts of fractions, percentages, and ratios, and demonstrating how to solve similar problems. Understanding these concepts is crucial in various fields, from everyday calculations to complex scientific analyses. We'll tackle different approaches to solve the problem, ensuring a comprehensive understanding for readers of all mathematical backgrounds.
Understanding the Problem: 6 of 250
The phrase "6 of 250" implies a part-to-whole relationship. We want to determine what fraction, percentage, or ratio 6 represents when compared to the whole, 250. This seemingly simple question opens the door to understanding several key mathematical concepts.
Approach 1: Fractions
The most straightforward approach is to express the relationship as a fraction. A fraction represents a part of a whole. In this case, 6 is the part, and 250 is the whole. Therefore, the fraction is 6/250.
This fraction can be simplified by finding the greatest common divisor (GCD) of 6 and 250. The GCD of 6 and 250 is 2. Dividing both the numerator (6) and the denominator (250) by 2, we get the simplified fraction 3/125.
Therefore, 6 out of 250 is equal to 3/125. This represents the precise mathematical relationship between 6 and 250.
Approach 2: Percentages
Percentages express a fraction as a portion of 100. To convert the fraction 6/250 to a percentage, we perform the following calculation:
(6/250) * 100%
This simplifies to:
0.024 * 100% = 2.4%
So, 6 out of 250 is 2.4%. This representation is useful for quickly understanding the relative proportion of 6 compared to 250. It clearly shows that 6 constitutes a small portion of the total.
Approach 3: Ratios
A ratio compares two quantities. In this case, the ratio of 6 to 250 can be written as 6:250 or 6/250. Similar to the fraction, this ratio can be simplified by dividing both numbers by their GCD (2), resulting in the simplified ratio 3:125.
Ratios are particularly useful when comparing different sets of data. For instance, if we have another set of data where we want to maintain the same proportion, we can use the simplified ratio 3:125 to scale the numbers accordingly.
Expanding the Understanding: Practical Applications
Understanding how to express a part-to-whole relationship using fractions, percentages, and ratios is crucial in many real-world scenarios. Consider the following examples:
-
Business and Finance: Calculating profit margins, market share, and investment returns all involve working with fractions and percentages. For example, if a company sells 6 out of 250 units produced, understanding the percentage (2.4%) helps in assessing sales performance.
-
Science and Statistics: Scientists often use ratios and percentages to represent experimental results or analyze data. For instance, in a clinical trial, the success rate of a drug might be expressed as a percentage or ratio.
-
Everyday Life: Calculating discounts, figuring out tips, or determining the proportion of ingredients in a recipe all rely on the same fundamental mathematical concepts. If a recipe calls for 6 spoons of sugar out of 250 spoons of total ingredients, we can easily express this as a percentage or ratio to adjust the recipe based on the quantity we want to make.
Further Exploration: Working with Larger Numbers and Decimals
The principles discussed above apply equally well to larger numbers and decimals. Let's consider an example with larger numbers: What is 60 out of 2500?
-
Fraction: 60/2500 simplifies to 3/125 (dividing by 20).
-
Percentage: (60/2500) * 100% = 2.4% Notice that the percentage remains the same. This highlights the consistency of the proportional relationship, regardless of the scale.
Now, let's introduce decimals: What is 6.5 out of 250?
-
Fraction: 6.5/250 can be simplified by multiplying both numerator and denominator by 2 to remove the decimal: 13/500. This fraction cannot be further simplified.
-
Percentage: (6.5/250) * 100% = 2.6%
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to calculate the percentage?
A1: The easiest way is to directly divide the part by the whole and then multiply by 100%. So, for 6 out of 250, it's (6/250) * 100% = 2.4%.
Q2: Can I use a calculator for these calculations?
A2: Absolutely! Calculators are very helpful, especially for more complex calculations involving larger numbers or decimals.
Q3: Why are fractions, percentages, and ratios important?
A3: They provide different ways to represent the relationship between a part and a whole. Fractions offer precision, percentages offer a quick comparison to 100, and ratios are useful for scaling or comparing different data sets. Understanding all three gives you a versatile toolset for solving various problems.
Q4: What if the numbers aren't easily divisible?
A4: If the numbers don't have a simple common divisor, you can still use a calculator to find the fraction, percentage, or ratio. The fraction might be a decimal fraction, but the percentage and ratio calculations remain straightforward.
Conclusion: Mastering Part-to-Whole Relationships
This article has explored the question "What is 6 of 250?" in depth, showing how to calculate the equivalent fraction, percentage, and ratio. We've also explored the practical applications of these concepts in various fields and answered frequently asked questions. The key takeaway is that understanding these mathematical concepts is essential not just for solving mathematical problems, but also for interpreting information and making decisions in various aspects of life. By mastering these tools, you'll be better equipped to tackle numerical challenges with confidence and clarity. Remember that the core concept is understanding the relationship between the part (6) and the whole (250), and the chosen method – fraction, percentage, or ratio – simply provides a different way of expressing that relationship.
Latest Posts
Latest Posts
-
How Long Until 9 50
Sep 17, 2025
-
How To Figure Out Ppm
Sep 17, 2025
-
Perimeter Of Triangle On Graph
Sep 17, 2025
-
What Is 30 Of 40000
Sep 17, 2025
-
Total Capacitance In Series Calculator
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.