What Is 6 Of 30000
wordexpert
Sep 24, 2025 · 5 min read
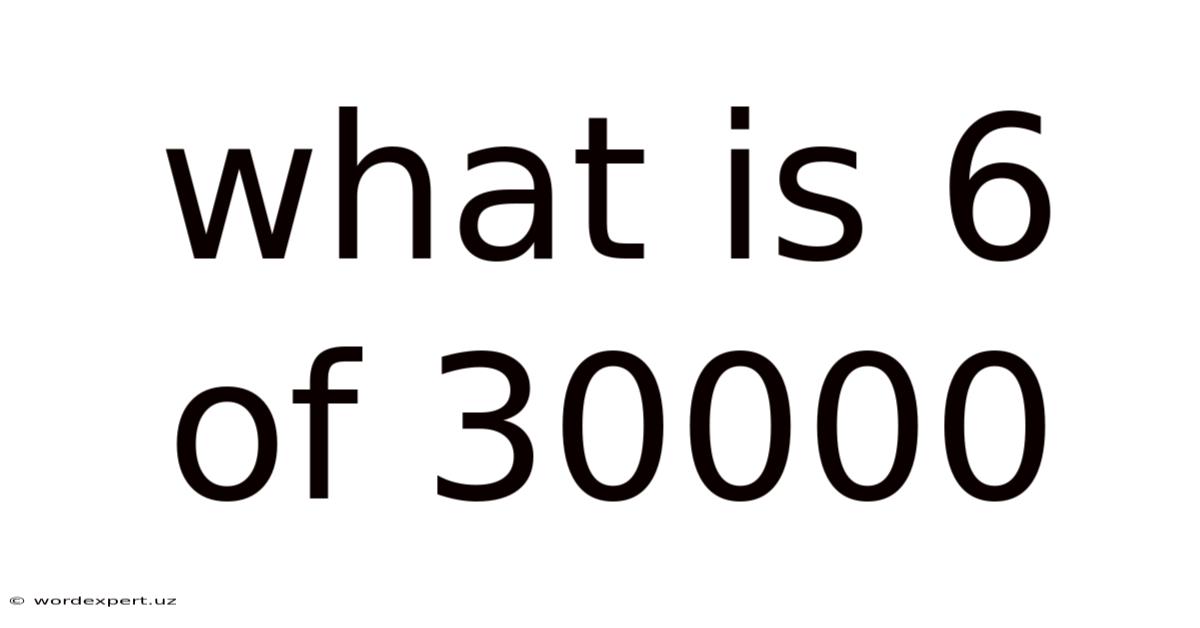
Table of Contents
What is 6 out of 30,000? Understanding Proportions and Percentages
This article explores the seemingly simple question: "What is 6 out of 30,000?" While the calculation itself is straightforward, understanding the implications of this proportion within larger contexts – like statistics, probability, and risk assessment – is crucial. We'll delve into the various ways to represent this ratio, explain the underlying mathematical principles, and explore real-world applications where understanding such small proportions is vital.
Introduction: Understanding Ratios and Proportions
At its core, "6 out of 30,000" represents a ratio. A ratio compares two quantities, showing their relative sizes. In this case, we're comparing the number 6 to the number 30,000. This can be expressed in several ways:
- As a fraction: 6/30,000
- As a decimal: Dividing 6 by 30,000 gives us 0.0002
- As a percentage: Multiplying the decimal by 100 gives us 0.02%
Each representation offers a different perspective on the relationship between the two numbers. The fraction is a direct representation of the ratio. The decimal provides a more concise numerical value, while the percentage offers an easily understood comparative measure relative to a whole (100%). Understanding these different representations is key to interpreting the significance of the ratio.
Calculating the Proportion: Step-by-Step
Let's break down the calculation into simple steps:
-
Express as a fraction: The simplest way to represent "6 out of 30,000" is as the fraction 6/30,000.
-
Simplify the fraction (optional): This fraction can be simplified by dividing both the numerator (6) and the denominator (30,000) by their greatest common divisor, which is 6. This simplifies the fraction to 1/5000. Simplifying the fraction makes it easier to understand the ratio in simpler terms.
-
Convert to a decimal: To convert the fraction to a decimal, divide the numerator by the denominator: 1 ÷ 5000 = 0.0002
-
Convert to a percentage: To convert the decimal to a percentage, multiply by 100: 0.0002 × 100 = 0.02%
Therefore, 6 out of 30,000 is equal to 1/5000, 0.0002, or 0.02%.
The Significance of Small Proportions
While 0.02% might seem insignificant at first glance, the context is crucial. In some situations, even a very small proportion can be extremely important. Consider these examples:
-
Medical Trials: In a drug trial with 30,000 participants, if 6 experience a serious side effect, that 0.02% rate needs careful scrutiny. While seemingly small, it might indicate a serious safety concern that requires further investigation. The rarity of the side effect doesn't negate its potential severity.
-
Manufacturing Defects: If a factory produces 30,000 units, and 6 are defective, that's a 0.02% defect rate. While seemingly small, it still represents a failure rate that needs addressing to maintain quality control and customer satisfaction. The cost associated with these 6 defective units, including replacements, repairs, and potential damage to reputation, can be significant.
-
Environmental Monitoring: If 6 out of 30,000 water samples show high levels of a pollutant, that small percentage indicates a potential environmental problem requiring attention. Even a low concentration of a harmful substance can have devastating long-term consequences.
-
Statistical Analysis: In statistical analysis, proportions are fundamental. Understanding small proportions helps researchers draw meaningful conclusions from data. A seemingly small difference in proportions between two groups might still be statistically significant, indicating a genuine difference.
Further Mathematical Concepts
Understanding 6 out of 30,000 also opens the door to exploring more advanced mathematical concepts:
-
Probability: The ratio can be interpreted as a probability. If you randomly select one item from a group of 30,000, the probability of selecting one of the 6 specific items is 0.02% or 1/5000.
-
Sampling and Inference: In statistical sampling, understanding the proportion of a sample that exhibits a certain characteristic allows us to make inferences about the larger population from which the sample was drawn. However, the accuracy of this inference is heavily dependent on the sample size and how representative the sample is of the population.
-
Error Rates: In fields like quality control, the proportion often represents an error rate. The lower the proportion, the lower the error rate, indicating a higher level of accuracy or precision.
Real-World Applications and Case Studies
The principle of understanding small proportions extends to numerous fields:
-
Finance: Analyzing investment returns, assessing risk, and determining the probability of default all involve working with proportions and percentages. A small percentage change in a large investment can have significant financial implications.
-
Epidemiology: Epidemiologists use proportions to track the spread of diseases, calculate infection rates, and assess the effectiveness of public health interventions. Even small changes in infection rates can be crucial in managing outbreaks.
-
Social Sciences: Researchers in social sciences employ proportions to analyze survey data, understand population demographics, and study social trends. Small differences in proportions can highlight significant social disparities or changes over time.
Frequently Asked Questions (FAQs)
-
Q: How do I calculate the percentage easily? A: The easiest way is to express the ratio as a fraction, convert the fraction to a decimal by dividing the numerator by the denominator, and then multiply the decimal by 100.
-
Q: Is 0.02% a significant proportion? A: The significance of 0.02% depends entirely on the context. In some scenarios, it might be negligible; in others, it could be incredibly important.
-
Q: How can I represent this ratio graphically? A: You can represent the ratio using a pie chart, bar graph, or other visual aids to easily illustrate the proportion of 6 compared to 30,000. A pie chart would show a tiny sliver representing the 6, highlighting its small proportion compared to the whole.
-
Q: What if the numbers were different? How would the calculation change? A: The same principles would apply. You would express the ratio as a fraction, simplify if possible, convert to a decimal, and then to a percentage.
Conclusion: The Importance of Context
The seemingly simple calculation of "6 out of 30,000" underscores the importance of context in interpreting numerical data. While 0.02% might seem insignificant, its impact can be profound depending on the situation. Understanding ratios, proportions, and percentages is essential in numerous fields, from science and engineering to finance and social sciences. Mastering these concepts allows us to analyze data effectively, draw meaningful conclusions, and make informed decisions in a wide variety of contexts. The ability to interpret and understand small proportions is a vital skill for critical thinking and problem-solving in today’s data-driven world. It's not just about the numbers; it's about understanding what those numbers mean within the bigger picture.
Latest Posts
Latest Posts
-
Calculation Of Et Tube Size
Sep 24, 2025
-
Swimsuit For My Body Type
Sep 24, 2025
-
25 Out Of 30 Grade
Sep 24, 2025
-
Cuantas Libras Son 95 Kilos
Sep 24, 2025
-
How Long Is 73 Days
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 Of 30000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.