What Is 60 Of 100
wordexpert
Sep 15, 2025 · 6 min read
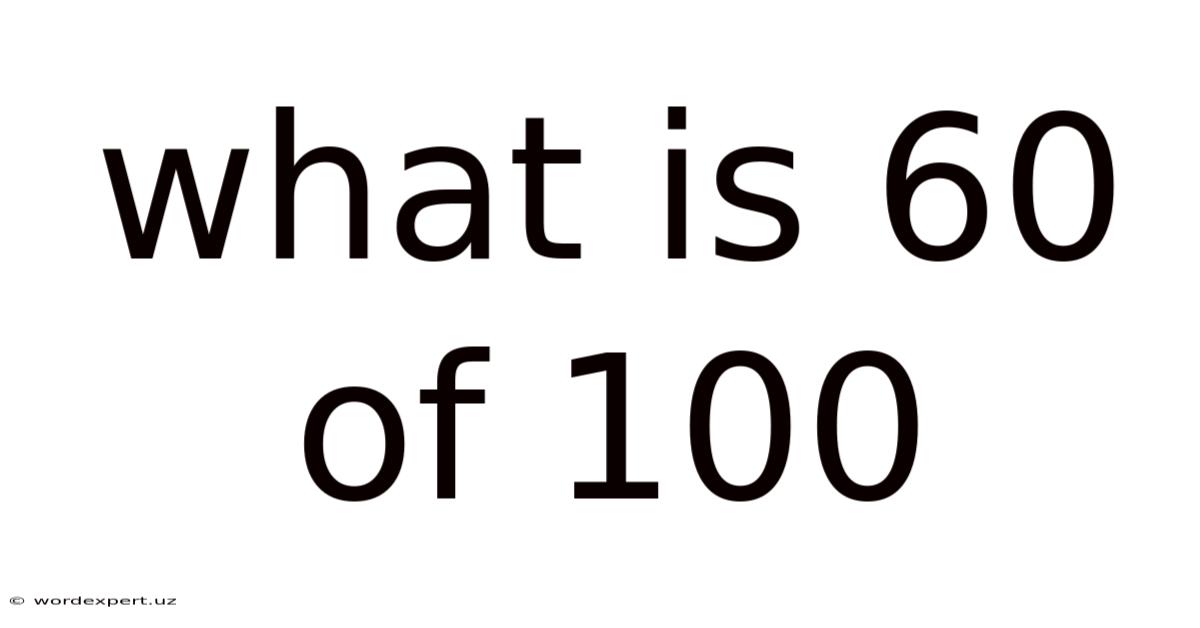
Table of Contents
What is 60 of 100? Understanding Percentages, Fractions, and Ratios
This article explores the seemingly simple question: "What is 60 of 100?" While the answer might seem obvious – 60 – a deeper dive reveals a wealth of mathematical concepts and their practical applications in everyday life. We'll unpack the meaning of this statement, exploring percentages, fractions, ratios, and their interconnectedness. We’ll also look at how this simple calculation applies to various real-world scenarios. This understanding is crucial for everything from calculating discounts to understanding financial reports.
Understanding Percentages
The phrase "60 of 100" is fundamentally a percentage. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, "60 of 100" is equivalent to 60%, which means 60 parts out of a total of 100 parts.
Key Concepts:
- Part: The specific amount being considered (in this case, 60).
- Whole: The total amount being referenced (in this case, 100).
- Percentage: The ratio of the part to the whole, expressed as a number out of 100.
Therefore, 60% represents the proportion 60/100. This fraction can be simplified to 3/5, indicating that 60 out of 100 is equivalent to three-fifths of the total.
Fractional Representation
As mentioned above, 60 of 100 can be represented as a fraction: 60/100. Fractions are a fundamental concept in mathematics, representing a part of a whole. The numerator (60) represents the part, and the denominator (100) represents the whole. This fraction can be simplified by finding the greatest common divisor (GCD) of 60 and 100, which is 20. Dividing both the numerator and the denominator by 20 gives us the simplified fraction 3/5.
This simplified fraction (3/5) is equally valid and often preferred as it's a more concise representation of the same proportion. Understanding how to simplify fractions is essential for working with ratios and percentages effectively.
Ratio Representation
A ratio compares the sizes of two or more quantities. In this case, the ratio of 60 to 100 can be expressed as 60:100. Similar to fractions, ratios can be simplified by dividing both sides by their GCD (20), resulting in a simplified ratio of 3:5. This means that for every 3 parts of one quantity, there are 5 parts of another. Ratios are often used to express proportions in various contexts, from recipes to map scales.
The relationship between fractions and ratios is very close; a fraction can be directly expressed as a ratio and vice versa. The fraction 60/100 is identical in meaning to the ratio 60:100.
Calculating Percentages: Beyond 60 of 100
Understanding "60 of 100" provides a foundation for calculating other percentages. The basic formula for calculating a percentage is:
(Part / Whole) * 100 = Percentage
For example, let's say you want to find what 30 is as a percentage of 50:
(30 / 50) * 100 = 60%
This demonstrates that 30 is 60% of 50. This formula is universally applicable for calculating any percentage, regardless of the numbers involved.
Real-world Applications
The understanding of percentages, fractions, and ratios derived from "60 of 100" has numerous practical applications:
- Discounts: A store offering a 60% discount means you pay 40% (100% - 60%) of the original price.
- Grades: A score of 60 out of 100 on a test represents a 60% grade.
- Surveys and Polls: If 60 out of 100 people surveyed prefer a particular product, that represents 60% preference.
- Financial Statements: Financial reports utilize percentages extensively to represent proportions of income, expenses, and assets.
- Statistics: Many statistical analyses rely on percentages and proportions to present data effectively.
- Mixing Ratios: In various fields, such as cooking or chemistry, accurate ratios are crucial. A 3:5 ratio (simplified from 60:100) might be used to mix ingredients.
Decimal Representation
The fraction 60/100, or its simplified form 3/5, can also be expressed as a decimal. To convert a fraction to a decimal, simply divide the numerator by the denominator:
60 ÷ 100 = 0.6
3 ÷ 5 = 0.6
Both calculations yield the same result: 0.6. Decimals are another way to represent parts of a whole, and they are commonly used in calculations and data representation.
Understanding Proportionality
The concept of "60 of 100" fundamentally illustrates proportionality. Proportionality refers to the relationship between two variables where their ratio remains constant. In this case, the ratio of the part to the whole (60:100 or 3:5) remains consistent regardless of the scale. If the whole were 200 instead of 100, the corresponding part would be 120 (maintaining the 3:5 ratio). This concept is crucial in scaling recipes, adjusting map scales, and various other applications.
Advanced Applications: Probability and Statistics
The understanding of proportions, directly linked to "60 of 100," is fundamental in probability and statistics. For example, if you have a bag with 100 marbles, 60 of which are red, the probability of picking a red marble at random is 60/100, or 60%. This concept extends to more complex scenarios in probability and statistical analysis.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 60/100?
A1: The simplest form of 60/100 is 3/5. This is obtained by dividing both the numerator and denominator by their greatest common divisor, which is 20.
Q2: How do I convert 60/100 to a decimal?
A2: To convert 60/100 to a decimal, divide 60 by 100. The result is 0.6.
Q3: How do I convert 60% to a fraction?
A3: To convert a percentage to a fraction, write the percentage as a fraction with a denominator of 100, and then simplify. So, 60% becomes 60/100, which simplifies to 3/5.
Q4: Can I use a calculator to solve percentage problems?
A4: Yes, calculators are very useful for solving percentage problems, especially when dealing with more complex calculations. Most calculators have a percentage function that simplifies the process.
Q5: What are some real-life examples beyond those mentioned?
A5: Many areas utilize this concept. Think about tax rates (e.g., a 6% sales tax), interest rates on loans, or the composition of alloys (a certain percentage of each metal).
Conclusion
While the question "What is 60 of 100?" initially seems straightforward, it serves as a gateway to understanding fundamental mathematical concepts – percentages, fractions, ratios, decimals, and proportionality. These concepts are not just abstract mathematical ideas; they are integral tools for navigating everyday life, making informed decisions, and interpreting data in various fields. Mastering these concepts provides a solid foundation for tackling more complex mathematical problems and real-world challenges. The seemingly simple answer of 60 unlocks a deeper understanding of numerical relationships and their widespread importance.
Latest Posts
Latest Posts
-
6 000 Meters In Miles
Sep 15, 2025
-
16 Mil Pasos A Km
Sep 15, 2025
-
Metric And Inches Conversion Chart
Sep 15, 2025
-
400 000 Pennies To Dollars
Sep 15, 2025
-
What Is 15 Of 4000
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.