What Is 65 Of 80
wordexpert
Sep 22, 2025 · 5 min read
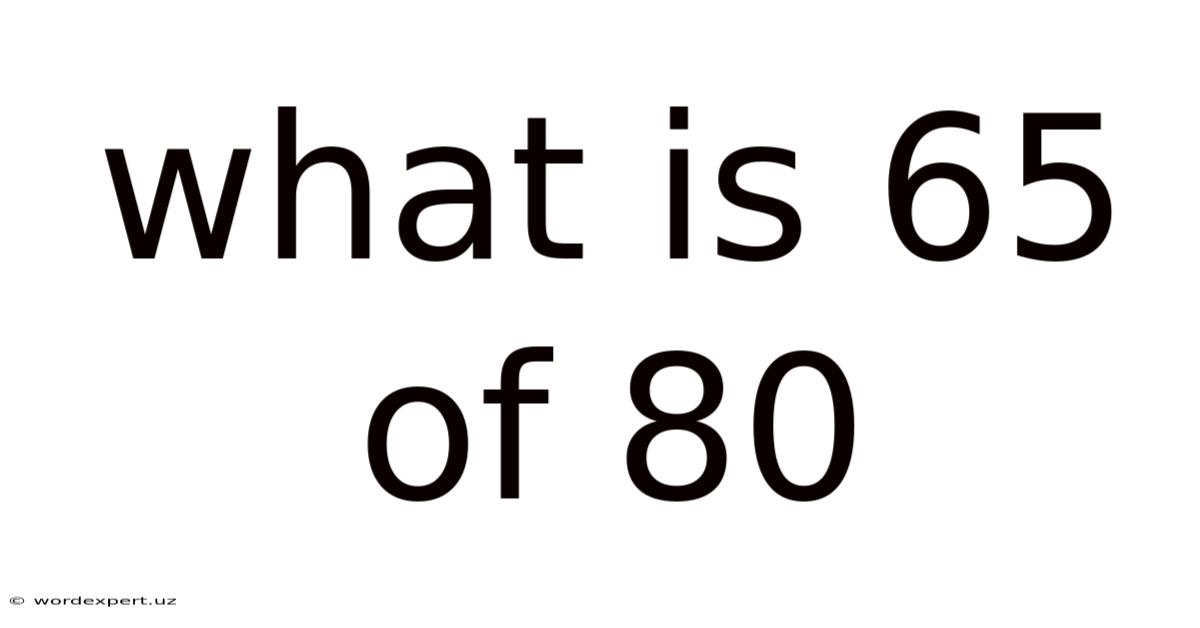
Table of Contents
What is 65% of 80? A Comprehensive Guide to Percentages and Their Applications
Finding 65% of 80 might seem like a simple calculation, but understanding the underlying principles of percentages opens the door to a vast world of applications in various fields, from everyday budgeting to complex financial modeling. This article delves into the methods of calculating percentages, explores the concept in depth, and provides real-world examples to solidify your understanding. We'll not only answer the question "What is 65% of 80?" but also equip you with the tools to tackle similar percentage problems with confidence.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of one hundred." Therefore, 65% means 65 out of 100, or 65/100. This fraction can be simplified to 13/20. This fundamental understanding is crucial for tackling percentage calculations.
Method 1: Using Decimal Conversion
This is arguably the most straightforward method for calculating percentages. It involves converting the percentage to a decimal and then multiplying it by the given number.
Steps:
-
Convert the percentage to a decimal: To convert 65% to a decimal, divide it by 100: 65 ÷ 100 = 0.65.
-
Multiply the decimal by the number: Multiply the decimal (0.65) by the number you want to find the percentage of (80): 0.65 × 80 = 52.
Therefore, 65% of 80 is 52.
Method 2: Using Fraction Conversion
This method utilizes the fractional representation of the percentage.
Steps:
-
Express the percentage as a fraction: As mentioned earlier, 65% can be written as 65/100.
-
Simplify the fraction (if possible): 65/100 simplifies to 13/20.
-
Multiply the simplified fraction by the number: Multiply the simplified fraction (13/20) by 80: (13/20) × 80 = 13 × (80/20) = 13 × 4 = 52.
Again, we arrive at the answer: 65% of 80 is 52.
Method 3: Using Proportions
This method utilizes the concept of proportionality. We set up a proportion where one ratio represents the percentage and the other represents the unknown value.
Steps:
-
Set up the proportion: We set up a proportion: 65/100 = x/80, where 'x' represents the unknown value (65% of 80).
-
Cross-multiply: Cross-multiply the terms: 65 × 80 = 100 × x
-
Solve for x: This gives us 5200 = 100x. Dividing both sides by 100, we get x = 52.
Therefore, 65% of 80 is 52.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in numerous real-world scenarios. Here are a few examples:
-
Sales and Discounts: Stores frequently offer discounts like "20% off." Knowing how to calculate percentages helps you determine the final price after a discount.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating these percentages accurately is crucial for budgeting and financial planning.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages helps you make informed financial decisions.
-
Tip Calculation: Calculating a tip in a restaurant usually involves finding a percentage of the bill.
-
Grade Calculation: Many educational systems use percentages to represent grades and overall performance.
-
Data Analysis: In statistics and data analysis, percentages are used to represent proportions and trends within datasets. For example, understanding the percentage of customers who prefer a particular product is essential for business strategy.
-
Financial Statements: Percentages are heavily used in financial statements like income statements and balance sheets to express ratios and analyze the financial health of a company. For instance, gross profit margin, net profit margin, and debt-to-equity ratios are all expressed as percentages.
Beyond the Basics: Advanced Percentage Calculations
While the methods above are sufficient for basic percentage calculations, more complex scenarios might require slightly different approaches. For example:
-
Finding the percentage increase or decrease: This involves calculating the difference between two numbers and expressing it as a percentage of the original number.
-
Calculating percentage change over time: This is often used to track trends in various metrics like sales, profits, or population growth.
-
Compound interest calculations: This involves calculating interest not only on the principal amount but also on the accumulated interest from previous periods.
Frequently Asked Questions (FAQ)
Q: How do I calculate a percentage of a number without a calculator?
A: You can use the fraction method or the proportion method described above. These methods don't require a calculator, although simplification might involve some manual calculation. For simpler percentages like 10%, 25%, or 50%, mental math can often suffice.
Q: What if the number I'm finding the percentage of is a decimal or a fraction?
A: The methods described above work equally well for decimals and fractions. Simply substitute the decimal or fraction into the calculation.
Q: Can I use a spreadsheet program like Microsoft Excel or Google Sheets to calculate percentages?
A: Yes, spreadsheet programs have built-in functions to calculate percentages easily. For example, in Excel, you would use the formula =A1*B1 where A1 contains the percentage (as a decimal) and B1 contains the number.
Q: Are there any online percentage calculators?
A: Yes, numerous websites offer free online percentage calculators. These can be helpful for quick calculations or verification of your work.
Conclusion
Calculating 65% of 80, which equals 52, is a relatively simple task. However, the underlying principles of percentage calculations are far-reaching and applicable in a wide range of situations. Understanding these principles not only allows you to solve specific percentage problems but also equips you with a fundamental skill for navigating the numerical aspects of daily life and various professional fields. Mastering percentage calculations will significantly enhance your ability to interpret data, make informed decisions, and solve problems efficiently across various domains. From personal finance to business analytics, the ability to work comfortably with percentages is an invaluable skill. Remember to practice regularly to strengthen your understanding and confidence in tackling percentage-based problems.
Latest Posts
Latest Posts
-
Twos Complement Binary To Decimal
Sep 22, 2025
-
What Grade Is A 7 11
Sep 22, 2025
-
35 000 Steps In Miles
Sep 22, 2025
-
Pile Ou Face En Ligne
Sep 22, 2025
-
Convert From Wavenumber To Wavelength
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 65 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.