What Is 70 Of 15
wordexpert
Sep 09, 2025 · 5 min read
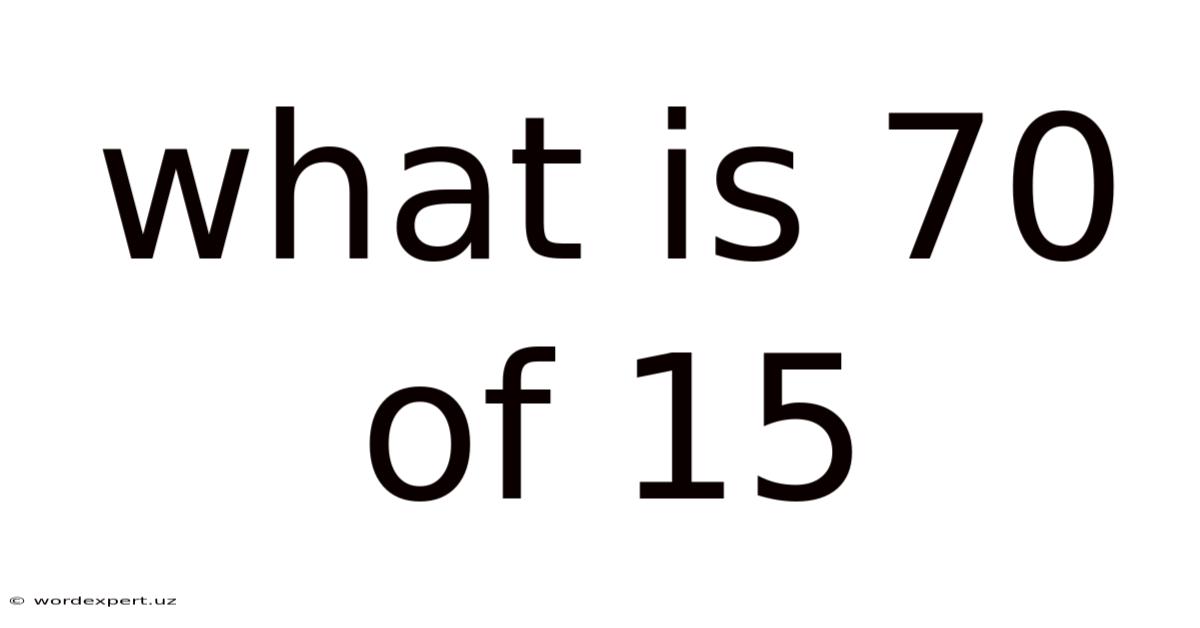
Table of Contents
What is 70% of 15? A Deep Dive into Percentages and Their Applications
Finding 70% of 15 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a wide range of applications in everyday life, from calculating discounts to understanding financial reports. This article will not only answer the question "What is 70% of 15?" but also delve into the mechanics of percentage calculations, explore different methods for solving such problems, and illustrate their relevance in real-world scenarios. We'll even touch upon some advanced concepts to enhance your understanding of this fundamental mathematical concept.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "per hundred." So, 70% means 70 out of 100, which can be written as the fraction 70/100 or the decimal 0.7. Understanding this fundamental concept is crucial for tackling any percentage problem.
Calculating 70% of 15: Three Approaches
There are several ways to calculate 70% of 15. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage (70%) into its decimal equivalent (0.7) and then multiply it by the number (15).
- Step 1: Convert 70% to a decimal: 70% = 70/100 = 0.7
- Step 2: Multiply the decimal by the number: 0.7 * 15 = 10.5
Therefore, 70% of 15 is 10.5.
Method 2: Using the Fraction Equivalent
We can also use the fraction equivalent of 70%, which is 70/100. This method involves multiplying the fraction by the number and simplifying the result.
- Step 1: Express 70% as a fraction: 70% = 70/100
- Step 2: Multiply the fraction by the number: (70/100) * 15
- Step 3: Simplify the expression: (70/100) * 15 = (7/10) * 15 = 105/10 = 10.5
Again, we arrive at the answer: 70% of 15 is 10.5.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between percentages and the whole. We set up a proportion:
- Step 1: Set up the proportion: x/15 = 70/100 (where x represents 70% of 15)
- Step 2: Cross-multiply: 100x = 70 * 15
- Step 3: Solve for x: 100x = 1050 => x = 1050/100 = 10.5
This confirms that 70% of 15 is 10.5.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are a few examples:
-
Discounts: Imagine a store offering a 70% discount on an item priced at $15. Using the methods described above, you would quickly determine that the discount amounts to $10.50, and the final price would be $4.50 ($15 - $10.50).
-
Taxes: Calculating sales tax or income tax often involves percentages. For instance, if the sales tax rate is 7%, you'd calculate 7% of the purchase price to determine the tax amount.
-
Tips: Calculating a tip in a restaurant usually involves finding a percentage of the total bill. A 20% tip on a $75 bill would be calculated as 20% of $75.
-
Financial Statements: Percentage changes are commonly used in financial statements to illustrate growth or decline in various metrics such as revenue, profit, and expenses. For example, a 10% increase in revenue signifies a notable improvement in a company's financial performance.
-
Grade Calculations: Percentages are frequently used in education to represent grades or scores. For example, a score of 70 out of 100 represents a grade of 70%.
-
Surveys and Statistics: Percentage is a fundamental tool in representing data in surveys and statistical analyses. For example, survey results might show that 70% of respondents prefer a particular product.
Beyond the Basics: Advanced Percentage Concepts
While finding 70% of 15 is a relatively simple calculation, understanding percentages extends to more complex scenarios. Here are some advanced concepts:
-
Finding the Percentage Increase or Decrease: These calculations involve determining the percentage change between two values. For example, if a value increases from 10 to 15, the percentage increase is calculated as [(15-10)/10] * 100% = 50%.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. Compound interest calculations are vital in understanding investments and loans.
-
Percentage Points vs. Percentage Change: It's crucial to differentiate between these two terms. A percentage point represents an absolute difference between two percentages, while a percentage change represents the relative change. For example, an increase from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
-
Working with Multiple Percentages: Often, calculations involve multiple percentage changes or discounts. For example, calculating the final price after applying a 20% discount followed by a 10% additional discount requires careful step-by-step calculation to avoid errors.
Frequently Asked Questions (FAQs)
Q1: What if I need to find a different percentage of 15?
A1: The methods described above can be adapted for any percentage. Simply replace 70% with the desired percentage and follow the same steps.
Q2: Can I use a calculator to solve percentage problems?
A2: Absolutely! Most calculators have a percentage function (%) that simplifies these calculations. Simply input the number, press the percentage button, and then multiply by the desired percentage.
Q3: Are there any online tools for calculating percentages?
A3: Yes, numerous online percentage calculators are readily available. These tools can be helpful for quick calculations and double-checking your work.
Q4: Why is understanding percentages important?
A4: Percentages are a fundamental aspect of mathematics with broad applications in numerous fields, including finance, business, science, and everyday life. A solid understanding of percentages is essential for making informed decisions and solving real-world problems.
Conclusion
Calculating 70% of 15, which equals 10.5, is a simple yet fundamental exercise that underscores the broader importance of understanding percentages. This seemingly basic calculation serves as a gateway to mastering a wide range of applications across various aspects of life. From understanding discounts and taxes to analyzing financial data and making informed decisions, the ability to work with percentages is a valuable skill that enhances both personal and professional capabilities. By grasping the fundamental principles and exploring the various methods for calculating percentages, you equip yourself with a powerful tool for navigating the quantitative world around you.
Latest Posts
Latest Posts
-
Weight Of 1 Liter Water
Sep 09, 2025
-
Whats 200 Ml In Cups
Sep 09, 2025
-
Conversion De Mililitros A Onzas
Sep 09, 2025
-
Gallons To Tons Of Water
Sep 09, 2025
-
Order Decimals Least To Greatest
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.