What Is 75 Of 5
wordexpert
Sep 16, 2025 · 6 min read
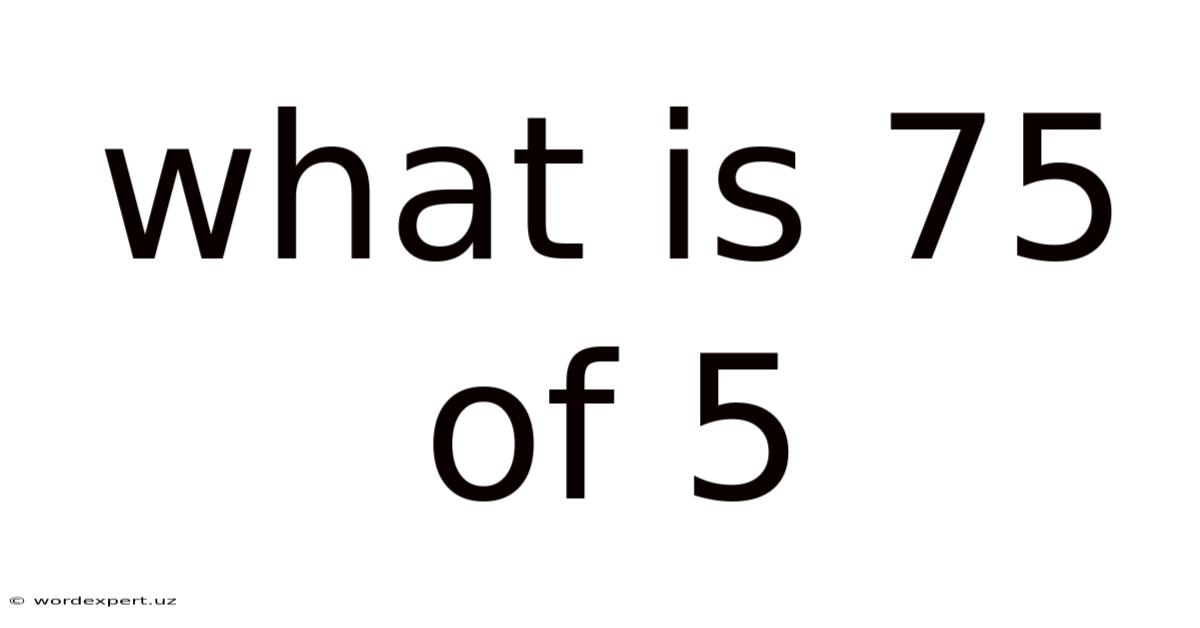
Table of Contents
What is 75% of 5? A Deep Dive into Percentages and Their Applications
Finding 75% of 5 might seem like a simple arithmetic problem, easily solvable with a calculator. However, understanding the underlying concepts of percentages and their practical applications opens a much wider world of mathematical understanding and problem-solving skills. This article will not only show you how to calculate 75% of 5 but also explore the core principles of percentages, different calculation methods, and real-world examples to solidify your understanding. This comprehensive guide will equip you with the knowledge to confidently tackle similar percentage problems in various contexts.
Understanding Percentages
Before we delve into the calculation, let's establish a firm grasp of what a percentage actually represents. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 75% means 75 out of 100, or 75/100. This can be further simplified to 3/4. Understanding this fundamental principle is key to solving percentage problems.
Calculating 75% of 5: Method 1 - Using Fractions
Since 75% is equivalent to 3/4, we can directly apply this fraction to find 75% of 5. This method offers a clear and intuitive approach, especially for those who are more comfortable working with fractions.
The calculation is as follows:
(3/4) * 5 = 15/4 = 3.75
Therefore, 75% of 5 is 3.75.
Calculating 75% of 5: Method 2 - Using Decimal Conversion
Another common method involves converting the percentage into its decimal equivalent. To do this, we divide the percentage by 100. For 75%, this translates to:
75% ÷ 100 = 0.75
Now, we simply multiply this decimal by the number we want to find the percentage of:
0.75 * 5 = 3.75
This method, again, confirms that 75% of 5 is 3.75.
Calculating 75% of 5: Method 3 - Using Proportions
Proportions offer a more structured approach, particularly useful for solving more complex percentage problems. We set up a proportion where one ratio represents the percentage and the other represents the unknown part relative to the whole.
Let 'x' represent 75% of 5. We can set up the proportion as follows:
75/100 = x/5
To solve for 'x', we cross-multiply:
75 * 5 = 100 * x
375 = 100x
x = 375/100
x = 3.75
Once again, the result confirms that 75% of 5 is 3.75.
Why Different Methods Matter
While all three methods yield the same result, each offers unique advantages. The fractional method provides a visual representation and is easily understandable for those comfortable with fractions. The decimal method is generally faster and more straightforward for those adept at decimal calculations. The proportion method, though perhaps slightly more involved, provides a structured framework that is especially helpful when dealing with more complicated percentage problems or when you need to clearly demonstrate your reasoning. Understanding multiple methods allows you to choose the most efficient and appropriate approach depending on the context of the problem.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial for navigating many aspects of daily life. Here are some common examples:
-
Sales and Discounts: Retail stores frequently advertise discounts as percentages. For example, a "25% off" sale means you'll pay 75% of the original price. The ability to quickly calculate these discounts is essential for making informed purchasing decisions.
-
Taxes and Interest: Calculating sales tax or interest on loans or investments requires a thorough understanding of percentages. Governments use percentages to levy taxes on income, goods, and services. Financial institutions use percentages to calculate interest earned on savings accounts or interest paid on loans.
-
Tips and Gratuities: In many cultures, it's customary to leave a tip or gratuity for service providers. These tips are typically expressed as a percentage of the total bill. Understanding how to calculate percentages quickly is valuable in these situations.
-
Grade Calculations: Academic grades are often expressed as percentages, representing the proportion of correct answers or the overall performance in a course. Students need to understand percentages to track their progress and assess their academic standing.
-
Data Analysis and Statistics: Percentages are fundamental to data analysis and statistics. They are used to represent proportions within data sets, making it easier to compare and interpret different variables. For instance, in surveys and polls, results are often reported as percentages to show the distribution of responses.
-
Financial Planning and Budgeting: Percentages play a vital role in personal finance. They are used to track savings, investment returns, budget allocation, and debt management. Understanding percentages helps you make informed financial decisions and plan for the future.
Beyond the Basics: More Complex Percentage Problems
While calculating 75% of 5 is a straightforward problem, the principles learned can be applied to more challenging scenarios. For example:
-
Finding the original value: If you know that 75% of a number is 3.75, how do you find the original number? This involves working backward using inverse operations.
-
Calculating percentage increase or decrease: If a value increases from 5 to 7, what is the percentage increase? This requires calculating the difference, then expressing that difference as a percentage of the original value.
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest over multiple periods.
-
Percentage change over time: Analyzing trends and growth patterns often requires calculating percentage changes over different time intervals.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method depends on individual preference and the specific problem. For simple problems, converting the percentage to a decimal and multiplying is often quickest. For more complex problems, setting up a proportion can provide a structured and clear approach.
Q: Can I use a calculator for percentage calculations?
A: Yes, calculators are valuable tools for percentage calculations, particularly for more complex problems. Most calculators have a percentage function (%) that simplifies the process.
Q: Are there any online tools or resources for calculating percentages?
A: Many websites and apps offer percentage calculators that can quickly solve percentage problems. These tools can be beneficial for verifying your calculations or for those who need assistance with more complex percentage problems.
Q: Why is it important to understand percentages?
A: Understanding percentages is vital for various aspects of life, from everyday financial transactions to more complex mathematical and statistical analysis. It allows for better decision-making in numerous scenarios.
Conclusion: Mastering Percentages for a Brighter Future
This article has explored the seemingly simple problem of calculating 75% of 5, but in doing so, we've uncovered a world of applications and deeper mathematical understanding. From the fundamental principles of percentages to the different calculation methods and real-world applications, we've covered a comprehensive range of concepts. Mastering percentages is not just about solving arithmetic problems; it's about developing critical thinking skills and gaining the ability to navigate numerous aspects of life with confidence and competence. The next time you encounter a percentage problem, remember the different approaches discussed here, and apply the method best suited to the task at hand. Remember, the ability to confidently calculate and interpret percentages is a valuable skill that will serve you well throughout your life.
Latest Posts
Latest Posts
-
How Long Until 7 00 Pm
Sep 16, 2025
-
Aortic Valve Annular Area Calculator
Sep 16, 2025
-
Born In 1962 How Old
Sep 16, 2025
-
10 Out Of 13 Percentage
Sep 16, 2025
-
How Long Should Toothpaste Last
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.