What Is 75 Of 6
wordexpert
Sep 23, 2025 · 5 min read
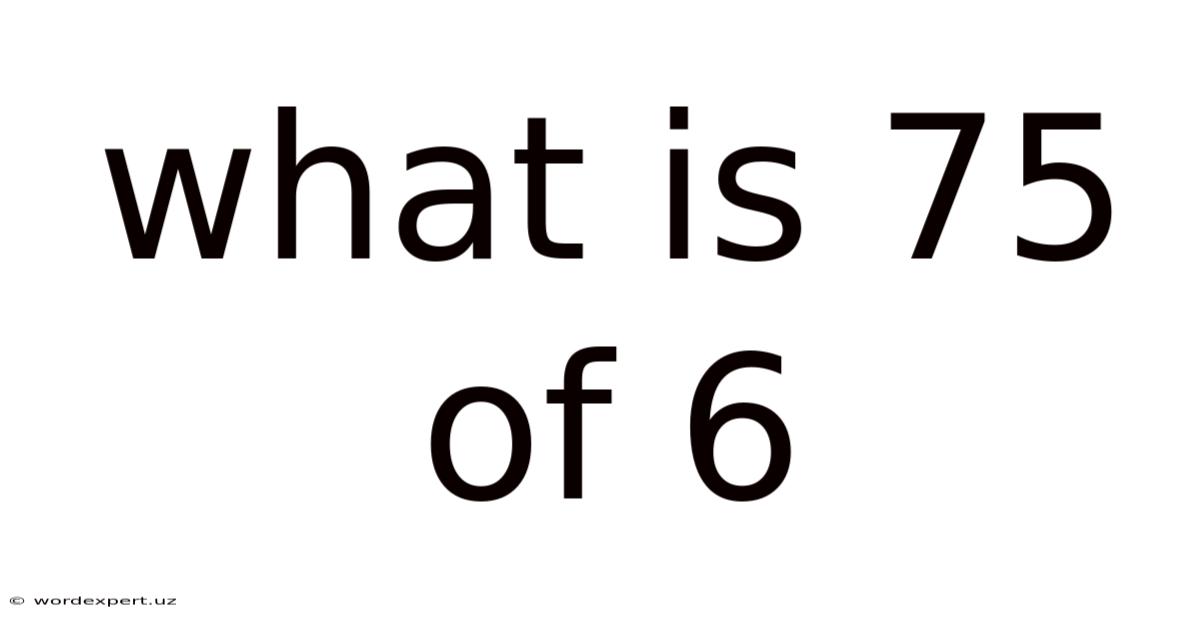
Table of Contents
What is 75% of 6? A Deep Dive into Percentages and Practical Applications
Finding 75% of 6 might seem like a simple calculation, but understanding the underlying principles of percentages unlocks a world of practical applications in everyday life, from calculating discounts to understanding financial reports. This article will not only show you how to calculate 75% of 6 but also explore the broader concept of percentages, different calculation methods, and real-world examples. We'll also delve into some frequently asked questions to solidify your understanding.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". So, 75% means 75 out of 100, which can be written as the fraction 75/100 or the decimal 0.75. Understanding this fundamental concept is crucial for calculating percentages efficiently.
Calculating 75% of 6: Three Methods
There are several ways to calculate 75% of 6. Let's explore three common approaches:
Method 1: Using the Fraction Method
As mentioned, 75% can be represented as the fraction 75/100. To find 75% of 6, we multiply 6 by this fraction:
6 * (75/100) = (6 * 75) / 100 = 450 / 100 = 4.5
Therefore, 75% of 6 is 4.5. This method is straightforward and easily understood.
Method 2: Using the Decimal Method
We can also convert 75% to its decimal equivalent, which is 0.75. Then, we simply multiply 6 by 0.75:
6 * 0.75 = 4.5
This method is often faster for those comfortable working with decimals.
Method 3: Using Proportions
This method is particularly useful for visualizing the relationship between the percentage and the whole. We can set up a proportion:
75/100 = x/6
Where 'x' represents the value we're trying to find (75% of 6). To solve for x, we cross-multiply:
100x = 75 * 6 100x = 450 x = 450 / 100 x = 4.5
This method highlights the underlying proportional relationship and can be helpful in understanding the concept of percentages more deeply.
Beyond the Basics: Expanding the Concept
While calculating 75% of 6 is a simple exercise, the principles involved have wide-ranging applications. Let's explore some real-world scenarios where understanding percentages is crucial:
-
Sales and Discounts: Imagine a store offering a 75% discount on an item originally priced at $6. Using our calculations, we know the discount is $4.50, and the final price would be $6 - $4.50 = $1.50.
-
Financial Literacy: Understanding percentages is essential for managing personal finances. Calculating interest rates on loans, savings accounts, and investments all involve percentage calculations. For example, if your investment grows by 10% annually, you need to understand percentages to determine the actual monetary increase.
-
Data Analysis and Statistics: Percentages are frequently used to represent data in reports, charts, and graphs. Understanding percentages allows you to interpret data effectively and make informed decisions based on the presented information. For instance, if a survey shows that 75% of respondents prefer a certain product, this represents a significant majority.
-
Science and Engineering: Percentages are commonly used in scientific calculations and engineering designs. For example, calculating the efficiency of a machine or the concentration of a chemical solution often involves percentage calculations.
-
Everyday Life: From calculating tips at restaurants to understanding tax rates, percentages are intertwined with many aspects of our daily lives. Mastering percentage calculations empowers you to make more informed decisions in various situations.
Different Percentage Calculations: Advanced Techniques
While we've focused on finding 75% of 6, let's briefly explore how to calculate other percentages:
-
Finding a percentage of a larger number: The same methods apply. For example, to find 25% of 200, you can use the fraction (25/100) * 200 = 50, the decimal 0.25 * 200 = 50, or the proportion method.
-
Finding the percentage one number represents of another: Suppose you scored 45 out of 60 on a test. To find the percentage, you would divide 45 by 60 and multiply by 100: (45/60) * 100 = 75%. This shows you scored 75% on the test.
-
Increasing or decreasing a number by a percentage: To increase a number by a percentage, add the percentage to 100%, convert to a decimal, and multiply by the original number. To decrease, subtract the percentage from 100%, convert to a decimal, and multiply. For instance, increasing 6 by 25% is 1.25 * 6 = 7.5, and decreasing 6 by 25% is 0.75 * 6 = 4.5.
Frequently Asked Questions (FAQ)
Q1: Why is understanding percentages important?
A1: Understanding percentages is fundamental for navigating many aspects of life, from managing finances and interpreting data to making informed decisions in various contexts. It's a crucial skill for academic success and professional advancement.
Q2: What if I need to calculate a percentage that isn't a simple multiple of 10?
A2: The same principles apply. You can use the fraction, decimal, or proportion methods regardless of the complexity of the percentage. For instance, to find 37% of 15, you'd calculate (37/100) * 15 or 0.37 * 15.
Q3: Are there any online calculators or tools to help with percentage calculations?
A3: Yes, many online calculators are available to assist with percentage calculations. However, understanding the underlying principles remains vital for problem-solving and critical thinking.
Q4: How can I improve my skills in calculating percentages?
A4: Practice is key! Try solving different percentage problems with varying numbers and percentages. You can find plenty of practice exercises online or in textbooks. Start with simple problems and gradually work towards more complex calculations.
Q5: Can percentages be used with numbers less than 1?
A5: Absolutely! The same principles apply. For example, 75% of 0.5 is 0.75 * 0.5 = 0.375.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 75% of 6, while seemingly trivial, serves as a gateway to understanding a powerful mathematical concept with far-reaching implications. Mastering percentages equips you with a valuable life skill, enhancing your ability to analyze data, manage finances, and make informed decisions across various domains. Through consistent practice and application, you can confidently navigate the world of percentages and unlock their practical potential in your personal and professional life. Remember, understanding the underlying principles is key—whether you're calculating discounts, interpreting statistics, or tackling more complex percentage-based problems.
Latest Posts
Latest Posts
-
What Is A 19 25 Grade
Sep 23, 2025
-
De C A F Grados
Sep 23, 2025
-
90 Days From June 23
Sep 23, 2025
-
Step Length Vs Stride Length
Sep 23, 2025
-
9 To The 6 Power
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.