What Is 75 Of 90
wordexpert
Sep 14, 2025 · 5 min read
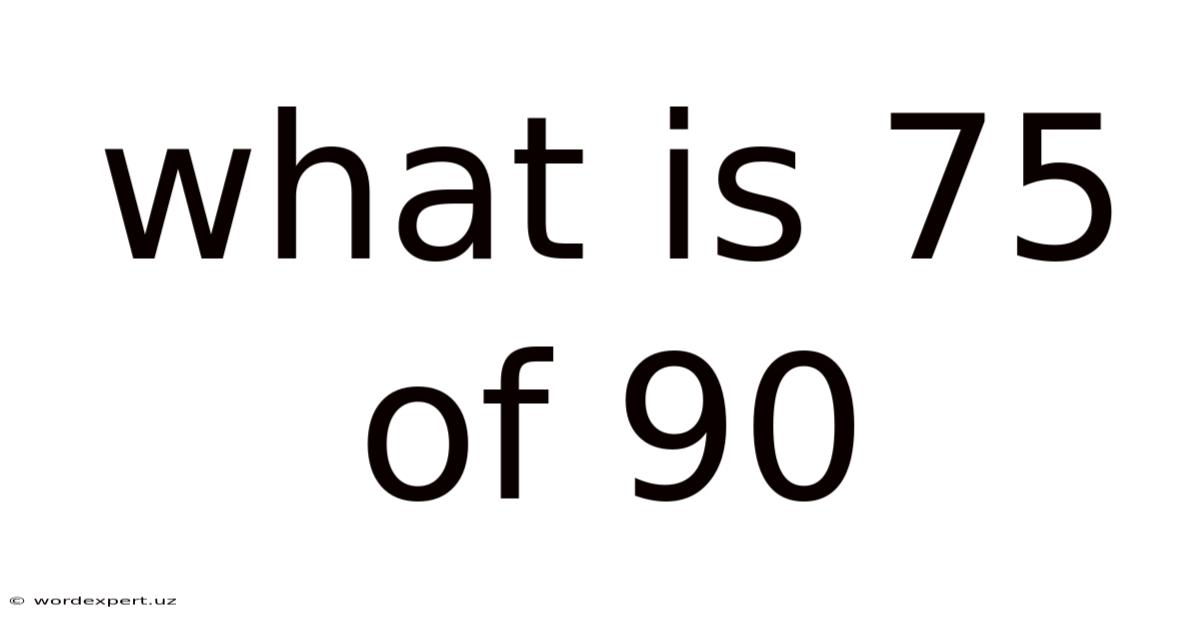
Table of Contents
What is 75% of 90? A Comprehensive Guide to Percentages and Their Applications
Finding 75% of 90 might seem like a simple arithmetic problem, but understanding the underlying principles of percentages unlocks a world of practical applications in various fields. This comprehensive guide will not only solve this specific problem but also delve into the broader concept of percentages, exploring different calculation methods, real-world examples, and frequently asked questions. By the end, you'll be confident in calculating percentages and applying this knowledge to various situations.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" – it represents a portion out of a whole divided into 100 equal parts. For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Understanding this basic definition is key to grasping percentage calculations.
Method 1: Using the Fraction Method to Calculate 75% of 90
This method involves converting the percentage to a fraction and then multiplying it by the number. Let's break down how to find 75% of 90:
-
Convert the percentage to a fraction: 75% can be written as 75/100. This fraction represents 75 parts out of a total of 100 parts.
-
Simplify the fraction (optional): The fraction 75/100 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 25. This simplifies to 3/4.
-
Multiply the fraction by the number: Now, multiply the simplified fraction (3/4) by 90:
(3/4) * 90 = 270/4 = 67.5
Therefore, 75% of 90 is 67.5.
Method 2: Using the Decimal Method to Calculate 75% of 90
This method involves converting the percentage to a decimal and then multiplying it by the number. Here's how:
-
Convert the percentage to a decimal: To convert 75% to a decimal, divide it by 100: 75/100 = 0.75
-
Multiply the decimal by the number: Now, multiply the decimal (0.75) by 90:
0.75 * 90 = 67.5
Again, we arrive at the answer: 75% of 90 is 67.5.
Method 3: Using Proportions to Calculate 75% of 90
This method uses the concept of proportions to solve the problem. A proportion is a statement that two ratios are equal. We can set up a proportion to find the unknown value (x), which represents 75% of 90:
75/100 = x/90
To solve for x, we cross-multiply:
75 * 90 = 100 * x
6750 = 100x
x = 6750/100
x = 67.5
This method confirms that 75% of 90 is 67.5.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in many everyday situations, including:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins all rely heavily on percentage calculations. For example, if a store offers a 25% discount on a $100 item, you would calculate 25% of $100 to determine the discount amount.
-
Statistics: Percentages are essential for representing data and interpreting statistical findings. For example, expressing survey results, election outcomes, or population demographics often involves using percentages.
-
Science: Percentages are used to express concentrations, error rates, and changes in measurements. For example, a chemist might express the concentration of a solution as a percentage.
-
Everyday Life: We encounter percentages daily, from calculating tips in restaurants to understanding sale prices in shops.
Beyond the Basics: Advanced Percentage Calculations
While finding 75% of 90 is a straightforward calculation, more complex scenarios might involve finding the percentage one number represents of another, calculating the original value before a percentage increase or decrease, or solving problems involving multiple percentages.
Example 1: Finding the Percentage One Number Represents of Another:
Let's say you scored 45 out of 60 on a test. To find the percentage you scored, you would divide the score obtained by the total possible score and multiply by 100:
(45/60) * 100 = 75%
Example 2: Calculating the Original Value After a Percentage Increase/Decrease:
If a price increased by 10% to reach $110, you would need to work backwards to find the original price. One approach is to use algebra:
Let x be the original price. Then:
x + 0.10x = $110
1.10x = $110
x = $110 / 1.10
x = $100
Therefore, the original price was $100.
Frequently Asked Questions (FAQ)
Q1: What are some common percentage shortcuts or tricks?
A1: Remembering that 10% of a number is simply dividing it by 10 can be helpful. From there, you can calculate other percentages based on multiples of 10%. For example, 20% is twice 10%, 5% is half of 10%, and so on.
Q2: How can I improve my percentage calculation skills?
A2: Practice is key! Start with simple problems and gradually move to more complex ones. Use different methods to solve the same problem to build your understanding and confidence. Online resources and practice exercises can be very helpful.
Q3: Are there any online calculators or tools available for percentage calculations?
A3: Yes, many online calculators and tools are readily available to assist with various percentage calculations. These tools can be particularly helpful for complex problems or when speed and accuracy are paramount.
Q4: What if the percentage is above 100%?
A4: A percentage above 100% simply means that the part is larger than the whole. This is often seen when comparing changes over time or when dealing with growth rates. For instance, a 120% increase indicates an increase of 20% more than the original value.
Conclusion: Mastering the World of Percentages
This comprehensive guide has explored the concept of percentages, demonstrated different calculation methods to find 75% of 90 (which is 67.5), and highlighted the wide range of applications for percentage calculations in various fields. By understanding the fundamentals and practicing regularly, you'll develop the skills needed to confidently tackle percentage-based problems in your daily life, academic pursuits, or professional endeavors. Remember, consistent practice is the key to mastering percentage calculations and unlocking their practical potential. The ability to understand and apply percentages is a valuable skill that will serve you well throughout your life.
Latest Posts
Latest Posts
-
Convert From Ksi To Mpa
Sep 14, 2025
-
What Is 20 Of 5
Sep 14, 2025
-
Area Of An Isosceles Trapezoid
Sep 14, 2025
-
What Is 3 4 Equivalent To
Sep 14, 2025
-
What Is 120 Days Ago
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.