What Is 80 Of 24
wordexpert
Sep 20, 2025 · 5 min read
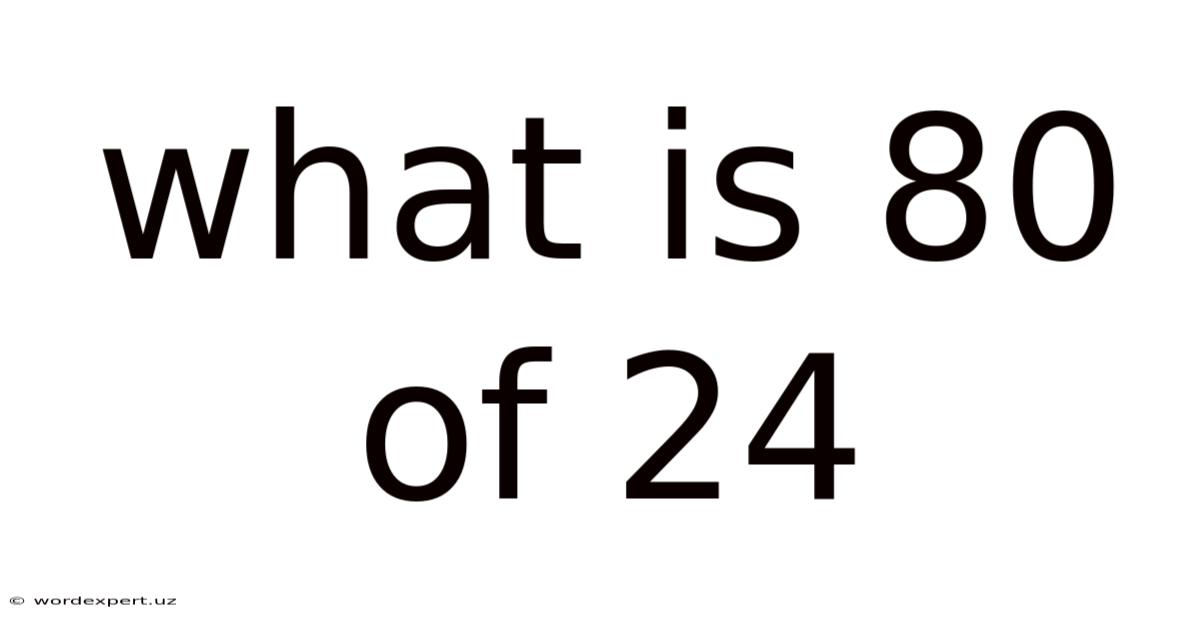
Table of Contents
What is 80% of 24? A Deep Dive into Percentages and Their Applications
Finding 80% of 24 might seem like a simple calculation, but it opens a door to a wider understanding of percentages, their applications in various fields, and the underlying mathematical principles. This article will not only answer the question directly but will also explore the different methods for calculating percentages, delve into the practical uses of percentages in everyday life and professional settings, and address common misconceptions. By the end, you'll be equipped to tackle any percentage problem with confidence.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). We represent percentages using the "%" symbol. Therefore, 80% means 80 out of 100, or 80/100, which simplifies to 4/5. This fundamental understanding is crucial for tackling percentage calculations.
Method 1: Using Decimal Conversion
The most straightforward method to calculate 80% of 24 involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100:
80% ÷ 100 = 0.8
Now, multiply this decimal by the number you're finding the percentage of:
0.8 × 24 = 19.2
Therefore, 80% of 24 is 19.2.
This method is efficient and readily applicable using a calculator or even mental math for simpler percentages.
Method 2: Using Fractions
As mentioned earlier, 80% can be expressed as the fraction 80/100, which simplifies to 4/5. We can use this fraction to calculate 80% of 24:
(4/5) × 24 = (4 × 24) / 5 = 96 / 5 = 19.2
This method reinforces the connection between percentages, fractions, and decimals, offering a deeper understanding of the underlying mathematical concepts. It's particularly useful when dealing with percentages that have easily simplified fractional equivalents.
Method 3: Proportion Method
The proportion method is a powerful technique for solving percentage problems, particularly when dealing with more complex scenarios. This method sets up a proportion:
Part / Whole = Percentage / 100
In our case:
x / 24 = 80 / 100
To solve for x (which represents 80% of 24), cross-multiply:
100x = 80 × 24 100x = 1920 x = 1920 / 100 x = 19.2
Therefore, using the proportion method, we again find that 80% of 24 is 19.2. This method is excellent for visualizing the relationship between the parts and the whole and is easily adaptable to different percentage problems.
Real-World Applications of Percentages
The concept of percentages permeates various aspects of daily life and professional fields. Here are a few examples:
-
Sales and Discounts: Retail stores frequently advertise discounts as percentages. For instance, a "20% off" sale indicates a reduction of 20% of the original price. Understanding percentage calculations allows consumers to determine the final price after the discount.
-
Finance and Investments: Percentages are fundamental in finance. Interest rates on loans and savings accounts are expressed as percentages. Understanding compound interest, which involves calculating percentages of increasingly larger amounts over time, is crucial for financial planning.
-
Taxes and Gratuities: Calculating sales tax, income tax, and service charges (tips or gratuities) all involve percentage calculations. These are essential for managing personal finances effectively.
-
Statistics and Data Analysis: Percentages are widely used in statistics to represent proportions, frequencies, and changes in data. Understanding percentages is crucial for interpreting statistical information accurately.
-
Science and Engineering: Percentages play a significant role in scientific calculations, expressing concentrations, efficiencies, and error margins. For example, determining the percentage purity of a chemical compound or the efficiency of a machine.
-
Health and Nutrition: Nutritional labels often express the percentage of daily recommended values for various nutrients. Understanding these percentages helps individuals make informed dietary choices.
Common Misconceptions about Percentages
Despite their seemingly simple nature, percentages can be a source of confusion. Here are some common misconceptions:
-
Adding Percentages Directly: A common mistake is to assume that adding percentages directly yields the correct result. For instance, a 10% increase followed by a 10% decrease does not result in the original value. This is because the second percentage is calculated on a changed base value.
-
Misinterpreting Percentage Changes: Percentage changes can be misleading if the context isn't clearly understood. A 100% increase doesn't necessarily mean doubling the original value. It only doubles the original value if the original value is positive, if it is a negative value the result will be zero.
-
Confusing Percentage Points with Percentages: A change of 10 percentage points is not the same as a 10% change. For example, moving from 20% to 30% is a 10 percentage point increase, but a 50% increase relative to the original value.
-
Ignoring the Base Value: The base value to which the percentage applies is critical. A 10% increase of a large number is significantly larger than a 10% increase of a small number.
Frequently Asked Questions (FAQs)
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new value and the original value, divide this difference by the original value, and multiply by 100. For a percentage decrease, follow the same procedure but use the absolute value of the difference to avoid a negative percentage result.
Q: How can I calculate the original value if I know the final value and the percentage change?
A: This requires working backward. If you know the final value and the percentage increase, divide the final value by (1 + percentage increase/100). For a percentage decrease, divide the final value by (1 - percentage decrease/100).
Q: What are some online tools or calculators for calculating percentages?
A: Numerous online percentage calculators are available. These tools can be useful for quick calculations, especially for more complex percentage problems. Many spreadsheet programs also have built-in functions for percentage calculations.
Conclusion: Mastering Percentages
Understanding percentages is a fundamental skill with far-reaching applications in various aspects of life. While finding 80% of 24 might seem trivial at first, mastering the different calculation methods and understanding the underlying principles provides a strong foundation for tackling more complex percentage problems. By recognizing common misconceptions and utilizing the appropriate methods, you can confidently navigate the world of percentages and apply this valuable skill to various real-world scenarios. Remember to always consider the context and the base value when dealing with percentages to avoid misinterpretations and ensure accuracy in your calculations.
Latest Posts
Latest Posts
-
M To Sq M Converter
Sep 20, 2025
-
What Is 62kg In Pounds
Sep 20, 2025
-
90 Days From 3 10
Sep 20, 2025
-
25 Percent Off 30 Dollars
Sep 20, 2025
-
Convert 9 Knots To Mph
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.