What Is 80 Of 9
wordexpert
Sep 23, 2025 · 5 min read
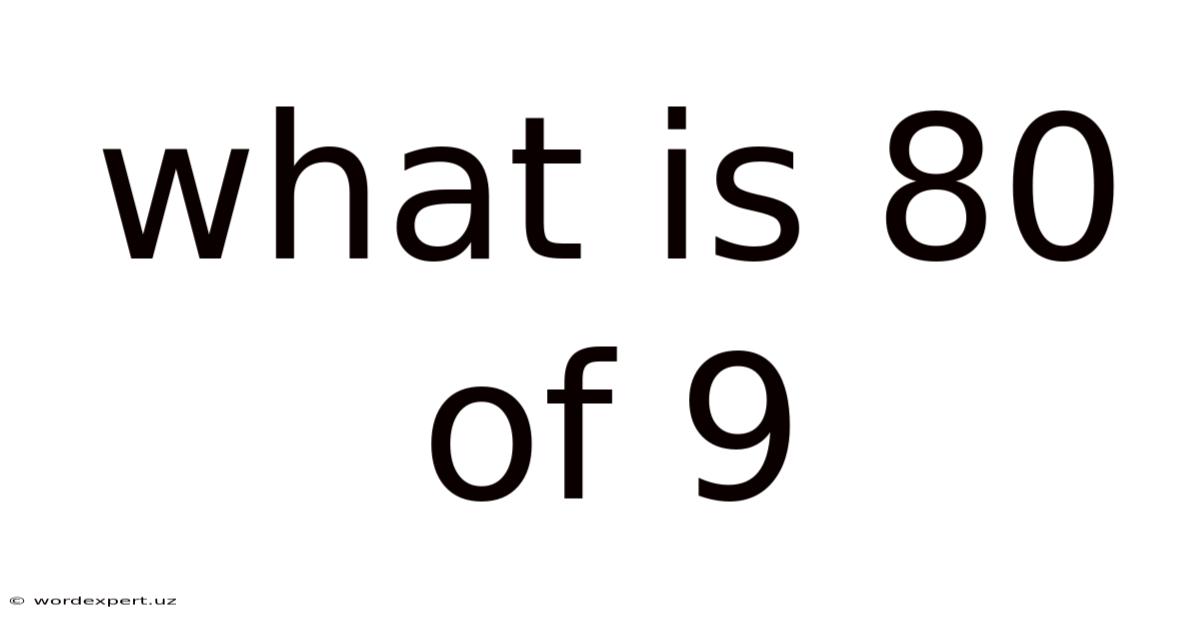
Table of Contents
What is 80% of 9? A Comprehensive Guide to Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and making financial decisions. This article will comprehensively explain how to calculate 80% of 9, providing a step-by-step approach, exploring the underlying mathematical principles, and demonstrating its practical relevance. We'll delve deeper than a simple calculation, exploring the concept of percentages, different calculation methods, and real-world applications. This guide is perfect for students, professionals, or anyone wanting a thorough grasp of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." So, 80% means 80 out of 100, or 80/100. This fraction can be simplified to 4/5. Understanding this fundamental concept is crucial for solving percentage problems.
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method for calculating percentages. We convert the percentage into a decimal and then multiply it by the number.
Steps:
-
Convert the percentage to a decimal: To convert 80% to a decimal, divide it by 100. 80% / 100 = 0.80 or simply 0.8
-
Multiply the decimal by the number: Now, multiply the decimal (0.8) by the number you want to find the percentage of (9). 0.8 * 9 = 7.2
Therefore, 80% of 9 is 7.2.
Method 2: Using Fractions
This method involves converting the percentage to a fraction and then multiplying it by the number.
Steps:
-
Convert the percentage to a fraction: As mentioned earlier, 80% is equivalent to 80/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 20. 80/100 simplifies to 4/5.
-
Multiply the fraction by the number: Now, multiply the simplified fraction (4/5) by the number (9). (4/5) * 9 = 36/5
-
Convert the improper fraction to a decimal: To get the decimal representation, divide the numerator (36) by the denominator (5). 36/5 = 7.2
Therefore, 80% of 9 is 7.2.
Method 3: Proportion Method
This method uses the concept of proportions to solve the problem.
Steps:
-
Set up a proportion: We can set up a proportion to represent the problem: 80/100 = x/9, where 'x' represents 80% of 9.
-
Cross-multiply: Cross-multiply the proportion: 80 * 9 = 100 * x
-
Solve for x: This gives us 720 = 100x. Divide both sides by 100 to solve for x: x = 720/100 = 7.2
Therefore, 80% of 9 is 7.2.
Comparing the Methods
All three methods – decimal conversion, fraction method, and proportion method – yield the same result: 7.2. The choice of method depends on personal preference and the context of the problem. The decimal conversion method is often the quickest for simple calculations, while the fraction method can be helpful for understanding the underlying mathematical relationships. The proportion method is particularly useful when dealing with more complex percentage problems.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in various real-life situations:
-
Retail Discounts: Calculating discounts on sale items. For example, if a $9 item is 80% off, the discount is $7.20, and the final price is $1.80 ($9 - $7.20).
-
Taxes and Fees: Determining the amount of tax or service charge added to a purchase price.
-
Financial Analysis: Calculating percentages of profit, loss, or growth in investments. Understanding percentage change is crucial for analyzing financial trends.
-
Data Analysis: Representing data in percentages for better visualization and interpretation. For instance, showing the percentage of students who passed an exam.
-
Scientific Measurements and Experiments: Percentages are frequently used in expressing experimental results and error margins in scientific research.
-
Tip Calculations: Easily calculate tips in restaurants or for service providers based on a percentage of the total cost.
Beyond the Basics: Understanding Percentage Change
Understanding percentage change is a crucial extension of basic percentage calculations. Percentage change signifies the relative increase or decrease in a value over time or between two points.
The formula for percentage change is: [(New Value - Old Value) / Old Value] * 100
For example, if a value increases from 9 to 10, the percentage change is: [(10 - 9) / 9] * 100 = 11.11% increase. Conversely, if the value decreases from 9 to 8, the percentage change is: [(8 - 9) / 9] * 100 = -11.11% decrease. Understanding percentage change allows for more in-depth analysis of trends and comparisons.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a different percentage of 9, say 25%?
A: You would follow the same methods, replacing 80% with 25%. Using the decimal method: 25%/100 = 0.25; 0.25 * 9 = 2.25. Therefore, 25% of 9 is 2.25.
-
Q: Can I use a calculator to find percentages?
A: Yes, most calculators have a percentage function (%) that simplifies the calculation. Simply input the percentage, then the multiplication sign (*), then the number.
-
Q: Are there any online tools to calculate percentages?
A: Yes, many websites and apps offer online percentage calculators that can handle various percentage calculations.
-
Q: How do I calculate the percentage one number represents of another?
A: To calculate what percentage one number (A) represents of another number (B), you use the formula: (A/B) * 100. For example, to find what percentage 2 is of 9: (2/9) * 100 ≈ 22.22%.
-
Q: What if I have a more complex percentage problem involving multiple percentages?
A: For more complex scenarios, it is recommended to break down the problem into smaller, manageable steps. Use the methods described above to calculate each step sequentially.
Conclusion
Calculating 80% of 9, which equals 7.2, is a seemingly simple calculation. However, understanding the underlying principles of percentages and their various calculation methods – including converting percentages to decimals or fractions, using proportions, and understanding percentage change – is crucial for numerous applications in everyday life, academics, and professional fields. Mastering these concepts empowers you to confidently tackle a wide range of percentage-related problems and enhances your analytical skills. By utilizing the methods described above and understanding their practical implications, you can confidently and effectively solve various percentage calculations and leverage this knowledge in your daily life. Remember, practice is key to mastering this fundamental mathematical skill.
Latest Posts
Latest Posts
-
90 Days From April 4th
Sep 23, 2025
-
Cuantas Libras Son 25 Kilogramos
Sep 23, 2025
-
How Many Days Until March
Sep 23, 2025
-
Cuantos Miligramos Tiene Una Cuchara
Sep 23, 2025
-
90 Days From Nov 25
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.