Whats 10 Percent Of 10000
wordexpert
Sep 21, 2025 · 5 min read
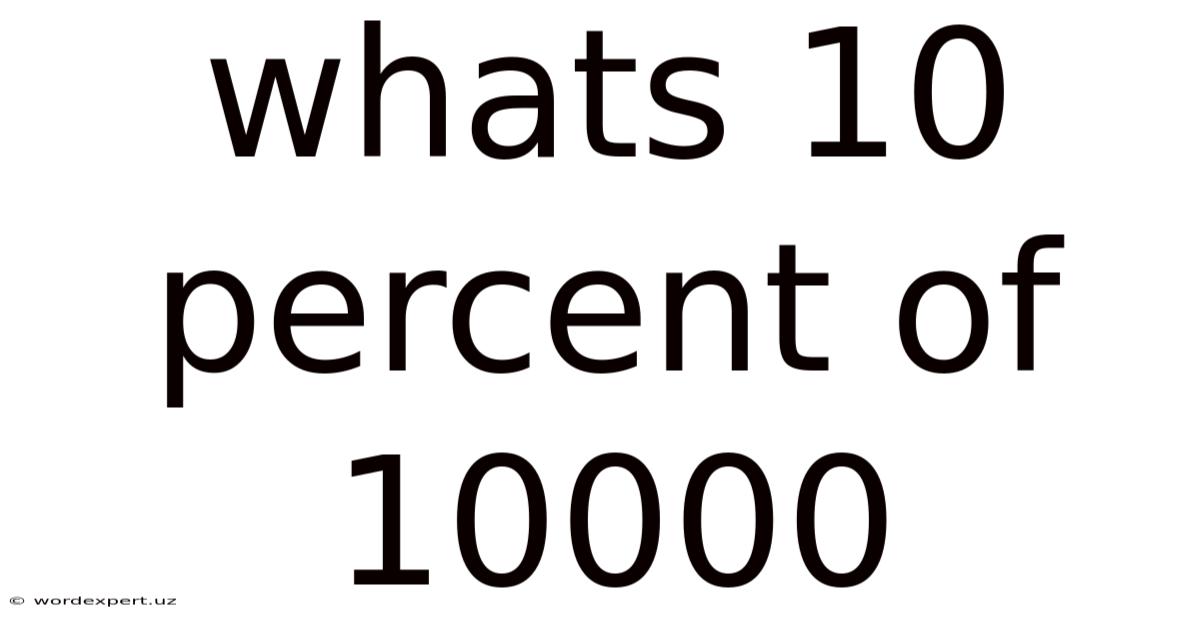
Table of Contents
What's 10 Percent of 10,000? A Deep Dive into Percentages and Their Applications
Finding 10 percent of 10,000 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various aspects of life, from budgeting and financial planning to understanding statistics and scientific data. This article will not only answer the question directly but also explore the concept of percentages, different methods for calculating them, and real-world applications to solidify your understanding.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." When we say "10 percent," we mean 10 out of every 100, or 10/100, which simplifies to 1/10. This fundamental understanding is key to solving percentage problems.
Calculating 10 Percent of 10,000: The Simple Method
The most straightforward way to calculate 10 percent of 10,000 is to multiply 10,000 by 10/100 (or 0.1).
10,000 x (10/100) = 10,000 x 0.1 = 1000
Therefore, 10 percent of 10,000 is 1000.
Alternative Methods: Flexibility in Calculation
While the previous method is efficient, understanding alternative approaches provides flexibility and a deeper grasp of percentages.
-
Using the Decimal Equivalent: As shown above, converting the percentage to its decimal equivalent (10% = 0.1) simplifies the calculation to a simple multiplication. This is often the quickest method.
-
Finding 1% and Scaling Up: First, find 1% of 10,000 by dividing 10,000 by 100. This equals 100. Then, multiply this value by 10 to find 10%. (100 x 10 = 1000). This method is helpful for understanding the proportional relationship between the percentage and the whole.
-
Using Proportions: This method involves setting up a proportion:
x/10000 = 10/100
Cross-multiplying, we get:
100x = 100000
Solving for x:
x = 100000/100 = 1000
This approach reinforces the concept of proportionality and is useful for more complex percentage problems.
Real-World Applications: Percentages in Everyday Life
Percentages are ubiquitous in daily life. Understanding them is essential for:
-
Financial Management: Calculating taxes, discounts (like a 10% sale!), interest rates on loans or savings accounts, tips at restaurants, and understanding profit margins in businesses all involve percentages. For instance, if you invest $10,000 and earn a 5% annual return, you'll have an extra $500 at the end of the year.
-
Statistics and Data Analysis: Percentages are used extensively to represent data in charts, graphs, and reports. Understanding percentages helps interpret statistical information accurately. For example, understanding unemployment rates (e.g., a 5% unemployment rate means 5 out of every 100 people are unemployed) requires a firm grasp of percentage calculation.
-
Scientific Applications: Percentages are used in various scientific fields to express concentrations, error rates, and changes in quantities. For example, calculating the percentage of a certain element in a compound, or determining the percentage change in a population over time.
-
Shopping and Sales: Discount percentages are frequently used in marketing and promotions. Knowing how to calculate discounts quickly allows for smarter shopping decisions. For example, a 20% discount on a $50 item reduces the price by $10, resulting in a final price of $40.
-
Grade Calculations: In education, percentage grades are frequently used to represent student performance. A 90% grade indicates a high level of mastery of the material, while a 60% grade suggests areas needing improvement.
Beyond the Basics: More Complex Percentage Problems
While calculating 10% of 10,000 is relatively simple, understanding more complex percentage problems requires additional skills. Here are some examples:
-
Finding the Percentage Increase or Decrease: Determining the percentage change between two values involves finding the difference between the values, dividing by the original value, and then multiplying by 100. For example, if a stock price increases from $100 to $120, the percentage increase is [(120-100)/100] x 100 = 20%.
-
Finding the Original Value: If you know a percentage of a value and the resulting amount, you can work backward to find the original value. For example, if 20% of a number is 40, you can divide 40 by 0.20 to find the original number (40/0.20 = 200).
-
Compound Percentages: These problems involve applying a percentage repeatedly over time. For example, calculating compound interest requires understanding how interest accrues on both the principal amount and the accumulated interest.
-
Percentage of a Percentage: Sometimes you need to find a percentage of a percentage. For instance, finding 5% of 20% of 10000 would be 100. This involves calculating the inner percentage first and then applying the outer percentage to the result.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a different percentage of 10,000?
A: Use the same methods described above, substituting the desired percentage for 10%. For example, to find 25% of 10,000, you would multiply 10,000 by 0.25 (or 25/100), resulting in 2500.
Q: Are there any online calculators available for percentage calculations?
A: Yes, many online calculators can perform percentage calculations. Simply search for "percentage calculator" on your preferred search engine. These calculators can be helpful for quick calculations and checking your work.
Q: What if the number I'm working with is not a nice round number like 10,000?
A: The same principles apply. Use a calculator to perform the multiplication or division as needed. The process remains identical, even if the numbers become more complex.
Q: How can I improve my understanding of percentages?
A: Practice is key! Work through various examples, starting with simple problems and gradually increasing the complexity. You can find plenty of practice problems online or in textbooks. Understanding the underlying concepts – fractions, decimals, and proportions – is also essential.
Conclusion: Mastering Percentages for Success
Understanding percentages is a fundamental skill that extends far beyond simple calculations. From managing personal finances to interpreting data and making informed decisions, the ability to work confidently with percentages is invaluable. By grasping the core concepts and practicing various methods of calculation, you'll gain a powerful tool for navigating the numerical aspects of everyday life and professional endeavors. Remember that even seemingly simple calculations like finding 10 percent of 10,000 offer a gateway to understanding more complex applications of percentages, ultimately enriching your understanding of the world around you.
Latest Posts
Latest Posts
-
How Old Is 10000 Days
Sep 21, 2025
-
How To Solve Ratio Problems
Sep 21, 2025
-
How Long Is 112 Weeks
Sep 21, 2025
-
Whats 20 Of 200 000
Sep 21, 2025
-
6 Million Minutes In Years
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Whats 10 Percent Of 10000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.