Whats 10 Percent Of 24
wordexpert
Sep 10, 2025 · 5 min read
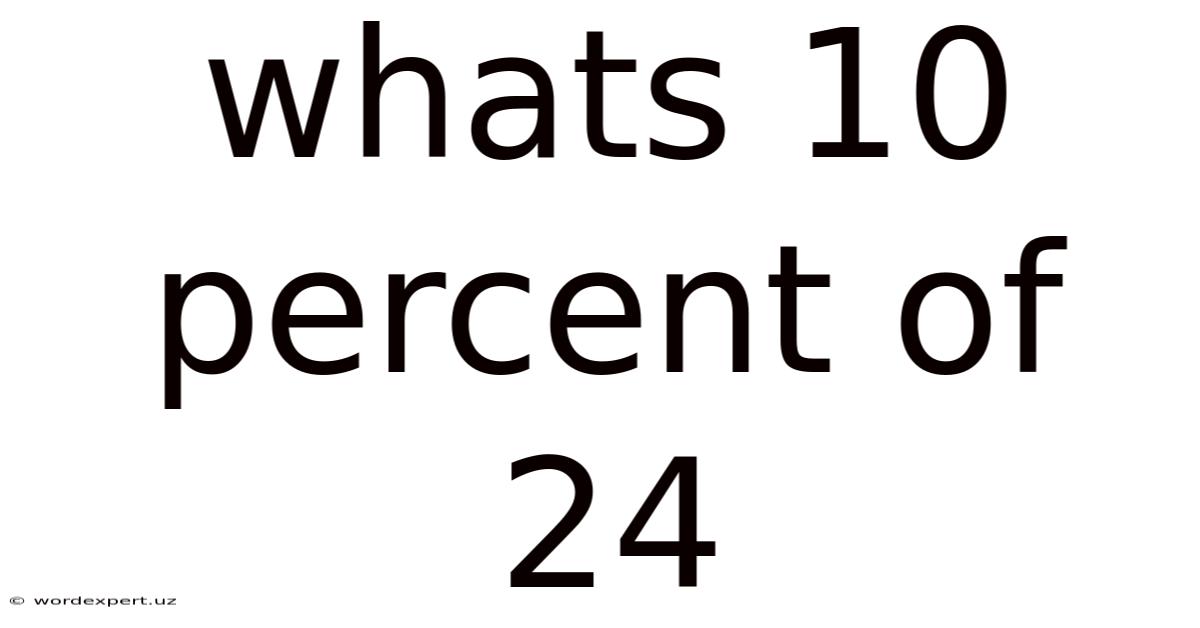
Table of Contents
What's 10 Percent of 24? A Deep Dive into Percentages and Their Applications
Finding 10 percent of 24 might seem like a simple calculation, easily solvable with a quick mental calculation or a calculator. However, understanding the underlying principles of percentages opens the door to a broader understanding of mathematical concepts crucial in various fields, from everyday budgeting to complex financial modeling. This article will not only answer the question "What's 10 percent of 24?" but will also explore the methods for calculating percentages, their practical applications, and delve into related mathematical concepts.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "per hundred." So, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. This fractional representation is key to understanding percentage calculations.
Method 1: Using the Fraction Method
The simplest way to find 10% of 24 is to utilize the fractional equivalent. As we established, 10% is equal to 1/10. Therefore, to find 10% of 24, we simply multiply 24 by 1/10:
24 x (1/10) = 24/10 = 2.4
Therefore, 10% of 24 is 2.4.
This method is particularly useful for percentages that have simple fractional equivalents, like 10%, 25%, 50%, and 75%. For instance, 25% is equivalent to 1/4, making it easy to calculate 25% of any number by dividing the number by 4.
Method 2: Using Decimal Conversion
Another common method involves converting the percentage into a decimal. To convert a percentage to a decimal, divide the percentage by 100. For 10%, this would be:
10% ÷ 100 = 0.10 or simply 0.1
Now, multiply this decimal by the number you want to find the percentage of:
24 x 0.1 = 2.4
Again, we arrive at the answer: 10% of 24 is 2.4. This method is versatile and works well with any percentage, regardless of its fractional simplicity.
Method 3: Using Proportions
The concept of proportions offers another powerful approach to calculating percentages. A proportion is a statement of equality between two ratios. We can set up a proportion to solve for 10% of 24:
Let x represent 10% of 24.
We can set up the proportion as follows:
10/100 = x/24
To solve for x, we can cross-multiply:
10 * 24 = 100 * x
240 = 100x
x = 240/100
x = 2.4
This confirms our previous results: 10% of 24 is 2.4. This method is particularly helpful in understanding the relationship between the percentage, the whole, and the part. It provides a clear visual representation of the problem.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-life scenarios:
-
Finance: Calculating interest on loans, savings accounts, and investments. Understanding discounts, sales tax, and tips. Analyzing financial statements and budgets.
-
Retail: Determining discounts and markups on products. Calculating profit margins and sales targets. Analyzing sales data and trends.
-
Science: Expressing experimental results, error margins, and statistical significance. Representing data in charts and graphs.
-
Everyday Life: Calculating tips in restaurants, understanding sales tax, determining discounts, managing personal finances, and much more.
Beyond the Basics: Exploring More Complex Percentage Problems
While finding 10% of 24 is straightforward, let's consider more complex scenarios to illustrate the versatility of percentage calculations:
Scenario 1: Finding a Different Percentage
Let's say we want to find 15% of 24. We can use any of the methods discussed above:
-
Fraction Method: While 15% doesn't have a simple fractional equivalent, we can use the decimal method or proportions.
-
Decimal Method: 15% converted to a decimal is 0.15. Therefore, 24 x 0.15 = 3.6. So, 15% of 24 is 3.6.
-
Proportion Method: 15/100 = x/24. Solving for x gives us x = 3.6.
Scenario 2: Finding the Percentage One Number Represents of Another
Let's say we have 6 out of 24 items. What percentage does this represent?
We can set up a proportion:
x/100 = 6/24
Cross-multiplying and solving for x gives us x = 25. Therefore, 6 represents 25% of 24.
Scenario 3: Percentage Increase and Decrease
Percentage increases and decreases are frequently encountered in various contexts. For example, if a price increases by 10%, we need to calculate the new price. If a price of $20 increases by 10%, the increase is 20 * 0.10 = $2. The new price is $20 + $2 = $22.
Conversely, if a price decreases by 10%, we subtract the decrease from the original price. A $20 price decreasing by 10% results in a $2 decrease, leading to a new price of $18.
The Importance of Accuracy and Precision
In many applications, particularly in finance and science, accuracy and precision in percentage calculations are paramount. Rounding errors can have significant consequences. It's crucial to use the appropriate number of decimal places based on the context of the problem.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method often depends on the specific percentage. For percentages with simple fractional equivalents (like 10%, 25%, 50%), the fraction method is quickest. For other percentages, the decimal method is generally straightforward and versatile.
Q: Can I use a calculator to calculate percentages?
A: Yes, most calculators have a percentage function (%) that simplifies the calculation. You can also use the decimal method by directly inputting the decimal equivalent of the percentage.
Q: How can I improve my understanding of percentages?
A: Practice is key. Try solving various percentage problems, starting with simple examples and gradually increasing the complexity. Understanding the underlying concepts of fractions, decimals, and proportions will strengthen your grasp of percentages.
Q: Are there any online resources for learning more about percentages?
A: Numerous online resources, including educational websites and videos, provide tutorials and practice exercises on percentages.
Conclusion
Calculating 10% of 24, while seemingly simple, serves as a gateway to understanding the broader world of percentage calculations. Mastering these calculations is crucial for success in various academic and professional fields. By understanding the different methods—using fractions, decimals, or proportions—you can confidently tackle a wide range of percentage problems, from simple calculations to more complex scenarios involving increases, decreases, and finding percentages represented by one number relative to another. The key is to practice regularly and to appreciate the underlying mathematical principles that govern these essential calculations. Remember, a solid understanding of percentages empowers you to make informed decisions in numerous aspects of life.
Latest Posts
Latest Posts
-
How Much Is 72 Hours
Sep 10, 2025
-
Convert Lb To Gallon Calculator
Sep 10, 2025
-
Chi Squared P Value Calculator
Sep 10, 2025
-
Pag Ibig Calculator Housing Loan
Sep 10, 2025
-
Calculate Doubling Time Of Cells
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Whats 10 Percent Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.