Whats 20 Percent Of 500
wordexpert
Sep 20, 2025 · 5 min read
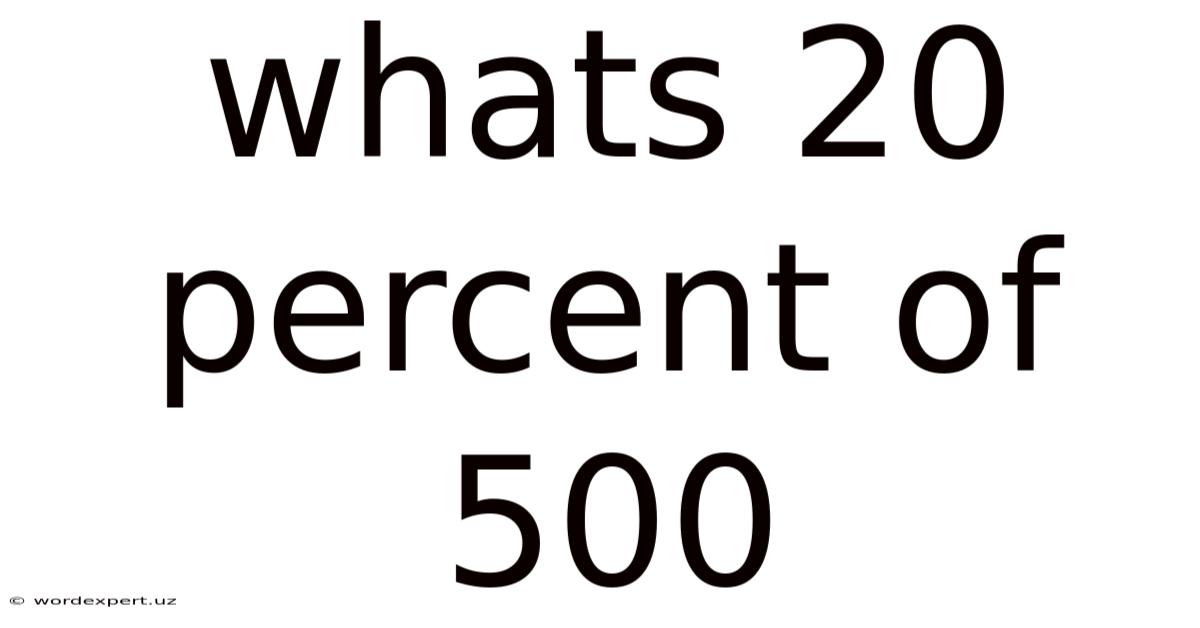
Table of Contents
What's 20 Percent of 500? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 500 might seem like a simple calculation, a quick task for a calculator. However, understanding the underlying principles of percentages goes far beyond this single problem. This article will not only answer the question "What's 20 percent of 500?" but will also explore the concept of percentages in depth, providing practical applications and addressing common misconceptions. We’ll delve into the mathematical foundations, discuss various methods of calculation, and explore real-world scenarios where this type of calculation is crucial. Mastering percentages is a fundamental skill with broad implications across various fields, from finance and budgeting to sales and statistics.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 20% means 20 out of 100, or 20/100, which simplifies to 1/5. This fraction represents a proportional relationship – a part relative to a whole.
Key Concepts:
- Whole: The total amount or quantity you're considering (in our case, 500).
- Part: The portion of the whole you are interested in finding (20% of 500).
- Percentage: The rate or proportion expressed as a number out of 100.
Calculating 20 Percent of 500: Three Methods
There are several ways to calculate 20% of 500. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
As mentioned, 20% is equivalent to the fraction 20/100 or 1/5. To find 20% of 500, we can multiply 500 by the fraction 1/5:
500 * (1/5) = 100
Therefore, 20% of 500 is 100.
Method 2: Converting Percentage to a Decimal
Percentages can be easily converted to decimals by dividing by 100. 20% divided by 100 is 0.20 (or simply 0.2). To find 20% of 500, we multiply 500 by 0.2:
500 * 0.2 = 100
Again, the answer is 100.
Method 3: Using the Proportion Method
This method utilizes the concept of ratios and proportions. We can set up a proportion:
20/100 = x/500
Where 'x' represents the unknown value (20% of 500). To solve for 'x', we can cross-multiply:
100x = 20 * 500 100x = 10000 x = 10000 / 100 x = 100
Once again, we arrive at the answer: 100.
Beyond the Calculation: Real-World Applications
Understanding percentages is vital in many real-world situations:
- Finance: Calculating interest on loans, savings accounts, and investments. For instance, a 20% interest rate on a $500 investment would yield $100 in interest.
- Sales and Discounts: Determining the price after a discount. A 20% discount on a $500 item would reduce the price by $100.
- Taxes: Calculating sales tax or income tax on earnings.
- Statistics: Analyzing data and expressing proportions within datasets. For example, understanding that 20% of a survey sample responded positively to a question.
- Profit Margins: Businesses use percentages to calculate profit margins, comparing profit to revenue.
- Tip Calculation: In many countries, it's customary to leave a tip (percentage of the total bill) for service staff.
- Grade Calculation: Many academic systems use percentages to represent grades or scores.
Advanced Percentage Calculations: Finding the Whole or the Percentage
While finding a percentage of a whole is straightforward, it’s equally important to understand how to calculate the whole amount given a percentage and its value, or to find the percentage given the part and the whole.
1. Finding the Whole:
Let's say you know that 20% of an unknown amount is 100. To find the whole amount, you can set up a proportion:
20/100 = 100/x
Cross-multiplying and solving for x:
20x = 10000 x = 500
This confirms that 100 is 20% of 500.
2. Finding the Percentage:
Suppose you spent $100 out of your total budget of $500. To determine the percentage spent, you can set up a proportion:
x/100 = 100/500
Cross-multiplying and solving for x:
500x = 10000 x = 20
Therefore, you spent 20% of your budget.
Common Percentage Mistakes and How to Avoid Them
Several common mistakes can occur when working with percentages:
- Incorrect Decimal Conversion: Failing to correctly convert a percentage to a decimal before multiplying. Remember to divide the percentage by 100.
- Misunderstanding the "of" in "x% of y": The word "of" always means multiplication.
- Confusing Percentage Increase/Decrease: A 20% increase followed by a 20% decrease does not result in the original value. The calculations are not symmetrical.
- Misinterpreting Percentage Points: Percentage points refer to the absolute difference between two percentages, not the relative change. For example, an increase from 20% to 25% is a 5 percentage point increase, but a 25% relative increase.
To avoid these errors, always carefully read the problem statement, double-check your calculations, and use multiple methods to verify your answers.
Frequently Asked Questions (FAQ)
Q: How do I calculate a different percentage of 500?
A: Use the same methods described above, substituting the desired percentage for 20%. For example, to calculate 35% of 500:
- Method 1 (Fraction): 35/100 * 500 = 175
- Method 2 (Decimal): 0.35 * 500 = 175
- Method 3 (Proportion): 35/100 = x/500; x = 175
Q: Can I use a calculator for these calculations?
A: Yes, calculators can simplify the calculations significantly, especially for more complex problems.
Q: Are there any online tools to calculate percentages?
A: Many online percentage calculators are available that can perform various percentage-related calculations instantly.
Q: What if I have a problem involving multiple percentages?
A: For problems involving multiple percentage changes or calculations, work one step at a time, ensuring accuracy in each step before proceeding.
Conclusion: Mastering the Power of Percentages
Understanding percentages is a fundamental skill with far-reaching applications. While finding 20% of 500 might seem trivial, the underlying principles are crucial for navigating various aspects of daily life, finance, and professional endeavors. By mastering the different calculation methods and avoiding common pitfalls, you can confidently approach percentage-related problems and gain a deeper understanding of their significance in the world around us. Remember to practice regularly to solidify your understanding and build your confidence in handling percentage calculations effectively. From simple everyday scenarios to complex financial analyses, the ability to work with percentages is an invaluable asset.
Latest Posts
Latest Posts
-
15 3 Ms In Scientific Nnotation
Sep 20, 2025
-
G Force In Car Accident
Sep 20, 2025
-
Cap Rate Calculation Real Estate
Sep 20, 2025
-
How Long Until 930 Am
Sep 20, 2025
-
60 Days From 11 8
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.