Whats 3 Percent Of 1000
wordexpert
Sep 21, 2025 · 5 min read
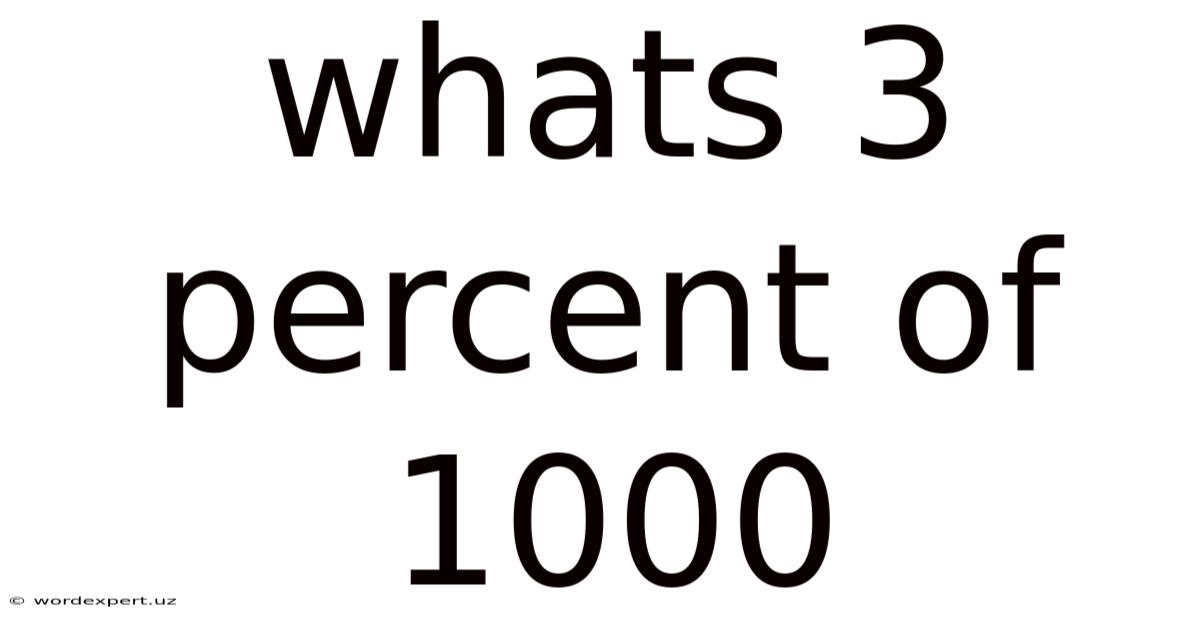
Table of Contents
What's 3 Percent of 1000? A Deep Dive into Percentages and Their Applications
Finding 3 percent of 1000 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications in various fields. This article will not only answer the question directly but will also explore the underlying principles of percentages, different methods of calculation, and real-world examples where this type of calculation proves invaluable. We will delve deeper than a simple answer, providing you with a comprehensive understanding of percentage calculations and their practical use.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." So, 3 percent (3%) means 3 out of every 100. This representation is incredibly useful for comparing proportions, analyzing data, and understanding changes or growth rates. Understanding percentages is crucial in many aspects of life, from calculating discounts and taxes to interpreting financial reports and understanding statistical data.
Calculating 3 Percent of 1000: Methods and Approaches
There are several ways to calculate 3% of 1000. Let's explore the most common methods:
Method 1: Using the Decimal Equivalent
The most straightforward approach involves converting the percentage to its decimal equivalent. To do this, we divide the percentage by 100. In this case:
3% ÷ 100 = 0.03
Now, we simply multiply this decimal by the total amount:
0.03 x 1000 = 30
Therefore, 3% of 1000 is 30.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 3% can be written as 3/100. To find 3% of 1000, we multiply the fraction by 1000:
(3/100) x 1000 = 30
This method demonstrates the inherent fractional nature of percentages. It provides another way to visualize the calculation.
Method 3: Proportion Method
This method utilizes the concept of ratios and proportions. We can set up a proportion:
3/100 = x/1000
To solve for x (which represents 3% of 1000), we cross-multiply:
100x = 3000
x = 3000/100
x = 30
This method reinforces the understanding that percentages represent a proportion of a whole.
Real-World Applications: Where Percentages Matter
The ability to calculate percentages is essential in numerous real-world scenarios. Let's explore a few examples:
-
Finance: Calculating interest on loans or investments, determining discounts on purchases, understanding tax rates, analyzing profit margins, and interpreting financial statements all rely heavily on percentage calculations. For example, a 3% interest rate on a $1000 investment would yield $30 in interest over a year (assuming simple interest).
-
Sales and Marketing: Understanding sales growth, tracking conversion rates, analyzing market share, and setting pricing strategies often involve working with percentages. A 3% increase in sales from the previous year represents a significant growth, while a 3% conversion rate means that 3 out of every 100 website visitors make a purchase.
-
Statistics and Data Analysis: Percentages are used extensively to present and interpret data. For example, 3% of a survey population holding a particular opinion would be a significant finding. Understanding percentage changes helps in tracking trends and making informed decisions.
-
Everyday Life: Calculating tips in restaurants, determining discounts during sales, figuring out the percentage of ingredients in a recipe, and even understanding nutritional information on food labels all involve percentage calculations.
Expanding the Concept: Beyond 3% of 1000
While we've focused on 3% of 1000, the principles discussed apply to any percentage and any amount. The methods described can be easily adapted to calculate other percentages. For example:
-
Calculating 15% of 500: Convert 15% to a decimal (0.15) and multiply by 500 (0.15 * 500 = 75).
-
Calculating 2.5% of 2000: Convert 2.5% to a decimal (0.025) and multiply by 2000 (0.025 * 2000 = 50).
Understanding the flexibility of these methods allows you to tackle a broad range of percentage problems.
Percentage Change: A Related Concept
Closely related to calculating percentages is understanding percentage change. This involves determining the percentage increase or decrease between two values. The formula for percentage change is:
Percentage Change = [(New Value - Old Value) / Old Value] x 100
For example, if a value increases from 1000 to 1030, the percentage change is:
[(1030 - 1000) / 1000] x 100 = 3%
This indicates a 3% increase. This concept is frequently used in various fields to track growth, decline, and fluctuations.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a percentage of a number that isn't a whole number?
A: The methods remain the same. Simply convert the percentage to a decimal and multiply it by the number, regardless of whether the number is a whole number or a decimal.
Q2: How can I calculate percentages quickly without a calculator?
A: For simple percentages, mental math tricks can be useful. For example, 10% of a number is easily found by dividing by 10. Other percentages can be derived from this base.
Q3: Are there any online tools or calculators to help with percentage calculations?
A: Yes, numerous online percentage calculators are available. These calculators can simplify complex calculations and provide quick results.
Q4: What is the difference between percentage points and percentages?
A: Percentage points represent the absolute difference between two percentages, while a percentage represents a relative change. For example, an increase from 10% to 13% is a 3-percentage point increase, but a 30% relative increase (3/10 x 100).
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a crucial skill applicable across numerous disciplines and daily life situations. Knowing how to calculate percentages accurately and efficiently allows you to interpret data, make informed decisions, and navigate various aspects of personal and professional life. We've shown that finding 3% of 1000 is just one application of these essential mathematical skills, a stepping stone to confidently tackling more complex percentage-related problems. By grasping the fundamentals, you equip yourself with a powerful tool for understanding and interacting with the world around you. From managing your finances to interpreting complex data sets, a solid understanding of percentages empowers you to make informed decisions and achieve your goals.
Latest Posts
Latest Posts
-
90 Days From June 2
Sep 21, 2025
-
Pounds To Cubic Feet Conversion
Sep 21, 2025
-
Cuantos Centimetros Tiene 1 Pie
Sep 21, 2025
-
Convert Rockwell C To Vickers
Sep 21, 2025
-
25 000 Hours To Days
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Whats 3 Percent Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.