Whats 30 Percent Of 80
wordexpert
Sep 21, 2025 · 5 min read
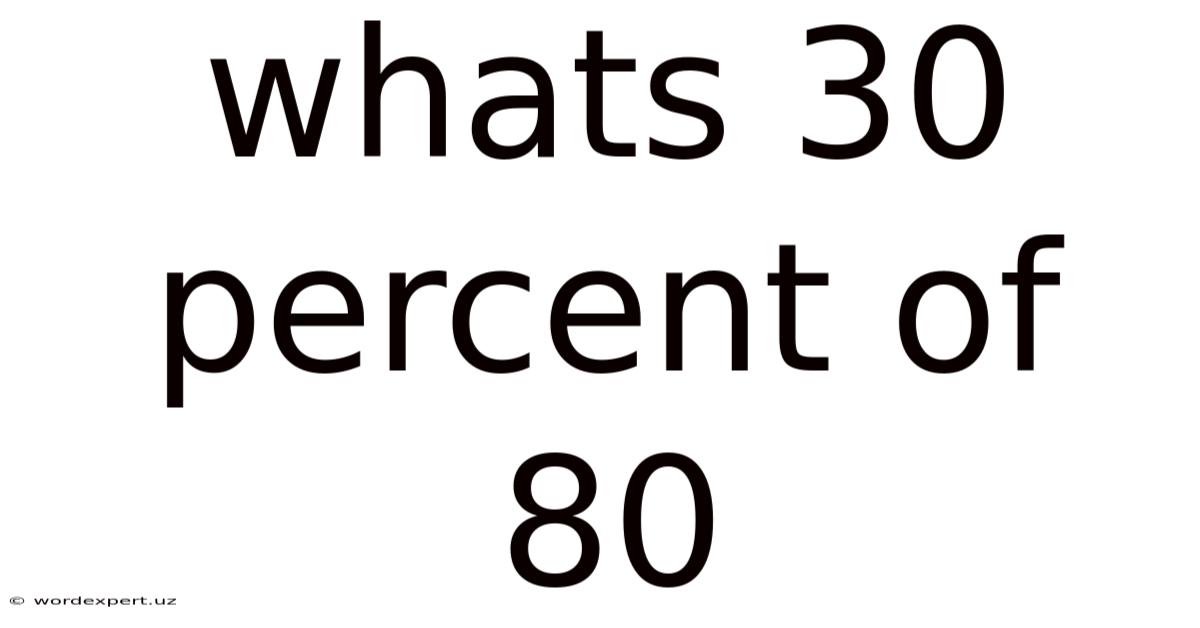
Table of Contents
What's 30 Percent of 80? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to advanced scientific analysis and financial modeling. Understanding how to determine a percentage of a number is crucial for making informed decisions and interpreting data accurately. This article will not only answer the question "What's 30 percent of 80?" but will also delve into the underlying principles of percentage calculations, explore various methods for solving such problems, and showcase the broad applicability of percentage calculations in real-world scenarios.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." Therefore, 30% means 30 out of 100, or 30/100, which simplifies to 3/10. This fundamental understanding forms the basis for all percentage calculations.
Method 1: Using Decimal Conversion
The most straightforward method for calculating 30% of 80 involves converting the percentage to a decimal. To do this, divide the percentage by 100. In this case:
30% ÷ 100 = 0.30
Now, multiply this decimal by the number you're finding the percentage of:
0.30 x 80 = 24
Therefore, 30% of 80 is 24. This method is simple, efficient, and easily adaptable for any percentage calculation.
Method 2: Using Fractions
Alternatively, we can use the fractional representation of the percentage. As mentioned earlier, 30% is equivalent to 30/100 or 3/10. We then multiply this fraction by the number:
(3/10) x 80 = 240/10 = 24
Again, we arrive at the answer: 30% of 80 is 24. This method provides a deeper understanding of the underlying mathematical principles involved.
Method 3: Using Proportions
Percentage problems can also be solved using proportions. A proportion is an equation that states that two ratios are equal. We can set up a proportion as follows:
30/100 = x/80
Where 'x' represents the unknown value (30% of 80). To solve for x, we cross-multiply:
30 x 80 = 100 x x
2400 = 100x
x = 2400/100
x = 24
This method reinforces the concept of equivalent ratios and provides another pathway to the solution: 30% of 80 is 24.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous real-life situations. Here are a few examples:
- Shopping and Sales: Determining the discount on sale items. If a shirt costs $80 and is on sale for 30% off, you'll save $24 (30% of $80).
- Taxes: Calculating sales tax or income tax. If the sales tax is 8%, you can easily determine the tax amount on a purchase.
- Finance: Calculating interest on loans or investments. Understanding interest rates and compound interest requires proficient percentage calculations.
- Data Analysis: Interpreting statistical data often involves working with percentages to understand trends and proportions. For example, understanding market share or survey results.
- Scientific Research: In fields like biology and chemistry, concentrations are often expressed as percentages.
- Everyday Budgeting: Tracking expenses and savings as a percentage of income helps maintain financial health. This allows for better financial planning and responsible spending habits.
- Grading Systems: Many educational systems use percentages to represent student performance. Understanding how percentages translate to grades is essential for both students and educators.
Beyond the Basics: More Complex Percentage Problems
While calculating 30% of 80 is relatively straightforward, many percentage problems involve more complex scenarios. Here are a few examples:
- Finding the Original Value: If an item is discounted by 30% and now costs $56, what was the original price? This requires working backward from the discounted price using inverse percentage calculations.
- Calculating Percentage Increase or Decrease: Determining the percentage change between two values, such as comparing sales figures from one year to the next.
- Compound Percentage Changes: Calculating the effect of multiple percentage changes applied sequentially, such as compound interest.
- Percentage of a Percentage: Determining a percentage of a percentage, for example, finding 20% of 40% of a value.
Solving More Complex Percentage Problems
Let's explore a more complex example: What is the final price of an item initially priced at $80 after a 30% discount followed by a 10% additional discount?
Step 1: Calculate the first discount.
30% of $80 = $24
Price after the first discount: $80 - $24 = $56
Step 2: Calculate the second discount based on the new price.
10% of $56 = $5.60
Price after the second discount: $56 - $5.60 = $50.40
Therefore, the final price after both discounts is $50.40. This demonstrates that sequential percentage changes do not simply add up; instead, each subsequent change is applied to the new value after the preceding change.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when calculating percentages?
A: Common mistakes include:
- Incorrect decimal conversion: Forgetting to divide the percentage by 100 before multiplying.
- Misinterpreting percentage increases/decreases: Incorrectly adding or subtracting percentages directly instead of applying them to the base value.
- Confusing percentage points with percentages: A change from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the original value.
Q: Are there any online calculators or tools that can help with percentage calculations?
A: Yes, many online calculators and spreadsheet software (like Microsoft Excel or Google Sheets) offer built-in functions for calculating percentages. These tools can save time and reduce the risk of errors, particularly for complex calculations.
Q: How can I improve my understanding of percentages?
A: Practice is key! Work through various percentage problems of increasing complexity, use different calculation methods to solidify your understanding, and explore online resources and tutorials for more in-depth explanations.
Conclusion
Calculating percentages is a fundamental mathematical skill with wide-ranging applications. Mastering this skill enables individuals to make informed decisions in various aspects of life, from personal finance and shopping to professional settings and academic pursuits. While the calculation of "30% of 80" serves as a simple introductory example, the principles discussed here lay the groundwork for tackling more complex percentage problems and mastering this essential life skill. Remember to practice regularly and utilize various methods to solidify your understanding. By doing so, you will not only be able to easily answer questions like "What's 30 percent of 80?" but also confidently navigate countless situations that require percentage calculations.
Latest Posts
Latest Posts
-
3 To The 8th Power
Sep 21, 2025
-
90 Days After August 14
Sep 21, 2025
-
How Much Longer Till 3 15
Sep 21, 2025
-
How Much Is 63 Kilograms
Sep 21, 2025
-
How Long Is 76 Weeks
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Whats 30 Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.