Whats 60 Percent Of 200
wordexpert
Sep 12, 2025 · 5 min read
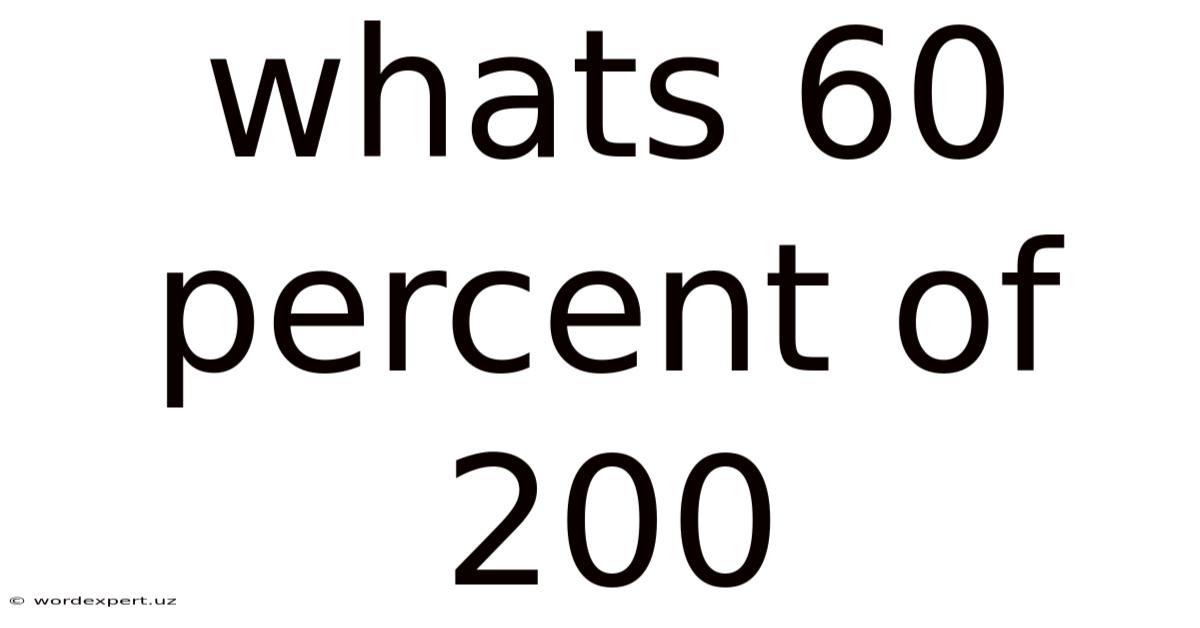
Table of Contents
What's 60 Percent of 200? A Deep Dive into Percentages and Their Applications
Finding 60 percent of 200 might seem like a simple task, a quick calculation easily done with a calculator. But this seemingly straightforward question opens the door to a broader understanding of percentages, their practical applications in everyday life, and the underlying mathematical principles. This article will not only answer the question directly but will also explore the various methods for calculating percentages, provide real-world examples, and delve into the conceptual understanding behind this fundamental mathematical concept.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin phrase "per centum," meaning "out of a hundred." Therefore, 60 percent means 60 out of 100, or 60/100, which simplifies to 3/5. Understanding this fundamental concept is crucial for grasping percentage calculations.
Calculating 60 Percent of 200: Three Methods
There are several ways to calculate 60 percent of 200. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. First, convert the percentage to its decimal equivalent by dividing by 100. 60 percent becomes 60/100 = 0.60 or simply 0.6. Then, multiply this decimal by the number you're finding the percentage of:
0.6 * 200 = 120
Therefore, 60 percent of 200 is $\boxed{120}$.
Method 2: Using Fractions
As mentioned earlier, 60 percent is equivalent to the fraction 60/100, which simplifies to 3/5. To find 60 percent of 200, multiply 200 by the fraction 3/5:
(3/5) * 200 = (3 * 200) / 5 = 600 / 5 = 120
Again, we arrive at the answer: $\boxed{120}$.
Method 3: Using Proportions
This method involves setting up a proportion. We can represent the problem as:
x / 200 = 60 / 100
To solve for x (60% of 200), cross-multiply:
100x = 60 * 200
100x = 12000
x = 12000 / 100
x = $\boxed{120}$
All three methods yield the same result: 60 percent of 200 is 120. Choosing the method that best suits your understanding and the context of the problem is key.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in our daily lives. Here are just a few examples:
-
Sales and Discounts: Stores frequently advertise discounts as percentages. For example, a "20% off" sale means you pay 80% of the original price. Understanding percentages helps you quickly calculate the final price.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the base amount. Knowing how to calculate percentages is essential for budgeting and financial planning.
-
Tips and Gratuities: Calculating tips in restaurants often involves determining a percentage of the total bill.
-
Interest Rates: Interest earned on savings accounts or paid on loans is typically expressed as a percentage.
-
Grade Calculations: Many academic systems use percentages to represent grades and overall performance. Understanding percentages is crucial for tracking academic progress.
-
Statistical Analysis: Percentages are fundamental to statistical analysis, allowing us to represent proportions and trends within data sets. This is crucial in fields like finance, market research, and public health.
-
Data Representation: Percentages provide a clear and concise way to represent proportions in various data sets, charts, and graphs. This helps with easy interpretation and understanding.
-
Financial Investments: Understanding percentage returns on investments is key to assessing the performance of different investment strategies.
-
Probability and Risk Assessment: Percentages are used extensively in probability calculations and risk assessment in many fields such as insurance and healthcare.
Beyond the Basics: More Complex Percentage Problems
While finding 60 percent of 200 is a relatively simple calculation, the principles extend to more complex scenarios. For example:
-
Finding the original amount: If you know that 60% of a number is 120, you can use the same principles to work backward and determine the original number. This involves setting up an equation: 0.6x = 120, and solving for x (x = 200).
-
Percentage increase or decrease: Calculating percentage changes involves finding the difference between two numbers and expressing that difference as a percentage of the original number. For instance, if a price increases from 100 to 120, the percentage increase is 20% [(120-100)/100 * 100%].
-
Compound interest: This involves calculating interest not just on the principal amount but also on the accumulated interest. Understanding percentages is crucial for accurately calculating compound interest over time.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage that's not a whole number, like 37.5%?
A: The same methods apply. Convert 37.5% to its decimal equivalent (0.375) and multiply by the number you're working with.
Q: Are there online calculators or software tools that can help with percentage calculations?
A: Yes, many online calculators and spreadsheet programs (like Microsoft Excel or Google Sheets) have built-in functions specifically designed for percentage calculations. These tools can be especially helpful for more complex problems.
Q: How can I improve my understanding of percentages?
A: Practice is key! Work through various percentage problems, starting with simple ones and gradually increasing the complexity. You can find many practice problems online or in textbooks. Understanding the underlying principles (fractions, decimals, and proportions) is also essential.
Conclusion: Mastering Percentages - A Lifelong Skill
The seemingly simple question, "What's 60 percent of 200?" has led us on a journey into the world of percentages, revealing their widespread applications and underlying mathematical concepts. Mastering percentage calculations is not just about solving mathematical problems; it’s about developing a crucial skill applicable to numerous aspects of life – from managing personal finances to understanding statistical data and making informed decisions in various contexts. By understanding the different methods and practicing regularly, you can confidently tackle percentage problems of all levels of complexity. The ability to easily calculate and interpret percentages is a valuable asset that will serve you well throughout your life.
Latest Posts
Latest Posts
-
400m Is How Many Feet
Sep 12, 2025
-
Area Of The Shaded Sector
Sep 12, 2025
-
Crl To Gestational Age Calculator
Sep 12, 2025
-
Reconstitution Of Powdered Drugs Formula
Sep 12, 2025
-
Convert Gallons To Square Feet
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 60 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.