1 4 Minus 1 2
wordexpert
Sep 23, 2025 · 5 min read
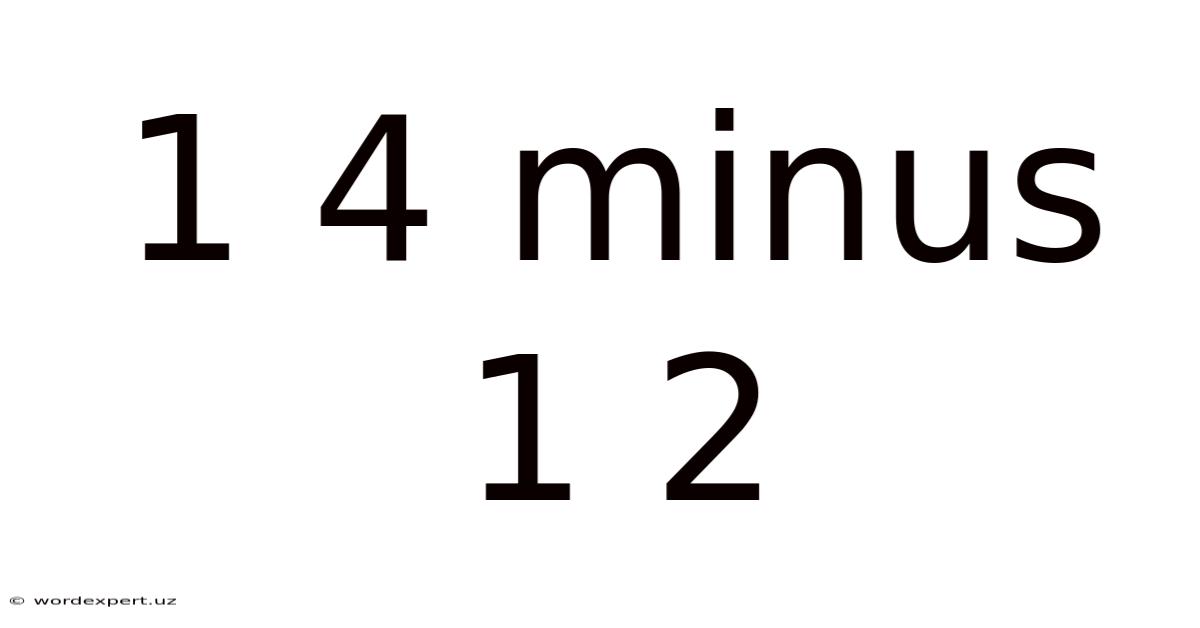
Table of Contents
Unraveling the Mystery: 1/4 Minus 1/2
This article delves into the seemingly simple yet surprisingly nuanced world of subtracting fractions, specifically tackling the common problem of 1/4 minus 1/2. We'll explore the mathematical principles behind the calculation, offering multiple approaches to solve it and building a solid understanding for anyone struggling with this fundamental concept in arithmetic. Understanding fraction subtraction is crucial for building a strong foundation in mathematics, impacting future learning in algebra, calculus, and beyond.
Understanding Fractions: A Quick Refresher
Before diving into the subtraction, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) means the whole is divided into four equal parts.
Method 1: Finding a Common Denominator
The most common method for subtracting fractions involves finding a common denominator. This means finding a number that is a multiple of both denominators. In our case, we need to find a common denominator for 4 and 2. The easiest approach is to find the least common multiple (LCM).
The multiples of 4 are: 4, 8, 12, 16... The multiples of 2 are: 2, 4, 6, 8...
The least common multiple of 4 and 2 is 4. Therefore, we will convert both fractions to have a denominator of 4.
- 1/4 already has a denominator of 4, so it remains unchanged.
- 1/2 needs to be converted. To change the denominator from 2 to 4, we multiply both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4
Now our subtraction problem becomes: 1/4 - 2/4
Since the denominators are the same, we can simply subtract the numerators: 1 - 2 = -1
Therefore, the answer is -1/4.
Method 2: Visual Representation
A visual approach can enhance understanding, particularly for those who are visually oriented learners. Imagine a pizza cut into four equal slices (quarters).
- 1/4 represents one slice of the pizza.
- 1/2 represents two slices of the pizza (since 1/2 is equivalent to 2/4).
If you try to take away two slices (1/2) from one slice (1/4), you'll end up owing one slice. This visually represents the negative result: -1/4.
Method 3: Converting to Decimals
Another approach involves converting the fractions to decimals before subtracting.
- 1/4 is equal to 0.25 (1 divided by 4).
- 1/2 is equal to 0.5 (1 divided by 2).
The subtraction then becomes: 0.25 - 0.5 = -0.25
Converting back to a fraction, -0.25 is equal to -1/4. This method highlights the equivalence between fractions and decimals.
Understanding the Negative Result
The negative result (-1/4) might seem counterintuitive at first. It simply signifies that we're attempting to subtract a larger quantity (1/2) from a smaller quantity (1/4). In the context of real-world problems, this negative result could represent a debt or a deficit. For instance, if you owe someone half a pizza (1/2) and only have a quarter of a pizza (1/4), you still owe them an additional quarter of a pizza.
Expanding the Concept: Subtracting Fractions with Different Denominators
The principles discussed above apply to subtracting any two fractions, regardless of their denominators. The key steps remain consistent:
- Find the least common denominator (LCM): Determine the smallest number that is a multiple of both denominators.
- Convert the fractions: Rewrite both fractions with the common denominator. Remember to multiply both the numerator and the denominator by the same factor to maintain the fraction's value.
- Subtract the numerators: Once the denominators are the same, subtract the numerators.
- Simplify the result: If possible, simplify the resulting fraction to its lowest terms.
Example: Subtract 2/3 from 5/6.
- LCM of 3 and 6 is 6.
- Convert the fractions: 2/3 becomes 4/6 (multiply both numerator and denominator by 2). 5/6 remains unchanged.
- Subtract the numerators: 5/6 - 4/6 = 1/6
- The result is already simplified: The answer is 1/6.
Further Applications and Real-World Examples
Understanding fraction subtraction is fundamental to various real-world applications. Here are some examples:
- Cooking: Adjusting recipes that call for fractional amounts of ingredients. If a recipe calls for 1/2 cup of sugar but you only have 1/4 cup, you'll need to adjust accordingly.
- Construction: Measuring and cutting materials accurately. Many construction projects require precise measurements involving fractions of an inch or foot.
- Finance: Calculating debts, profits, and losses. Understanding fractions is crucial for managing personal finances effectively.
- Science: Many scientific calculations involve fractional measurements and data analysis.
Frequently Asked Questions (FAQ)
Q: What if I get a negative fraction?
A: A negative fraction simply means you're subtracting a larger fraction from a smaller one. It represents a deficit or debt, as explained previously.
Q: Can I use a calculator to solve fraction subtraction problems?
A: Yes, many calculators have fraction functions that can simplify the process. However, understanding the underlying mathematical principles is essential for building a strong foundation in mathematics.
Q: Why is finding a common denominator important?
A: Finding a common denominator allows us to express the fractions in a consistent unit of measurement, making subtraction (or addition) of the numerators straightforward. You cannot directly subtract numerators if the denominators are different because the fractions represent parts of differently sized wholes.
Conclusion
Subtracting fractions, even a seemingly simple problem like 1/4 minus 1/2, requires a solid understanding of fundamental mathematical concepts. By mastering the techniques of finding a common denominator, utilizing visual representations, or converting to decimals, you can confidently tackle a wide range of fraction subtraction problems. Remember that practice is key to building fluency and confidence in your mathematical abilities. Through consistent effort and a clear understanding of the underlying principles, you can unlock the world of fractions and progress to more advanced mathematical concepts. The ability to confidently work with fractions will serve you well throughout your academic journey and beyond, empowering you to solve problems in various real-world scenarios.
Latest Posts
Latest Posts
-
6to The Power Of 2
Sep 24, 2025
-
30 Days From March 17th
Sep 24, 2025
-
45 Days From April 25
Sep 24, 2025
-
What Is 40 Of 10000
Sep 24, 2025
-
Umol L To Mg L
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Minus 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.