2 Square Root Of 6
wordexpert
Sep 22, 2025 · 6 min read
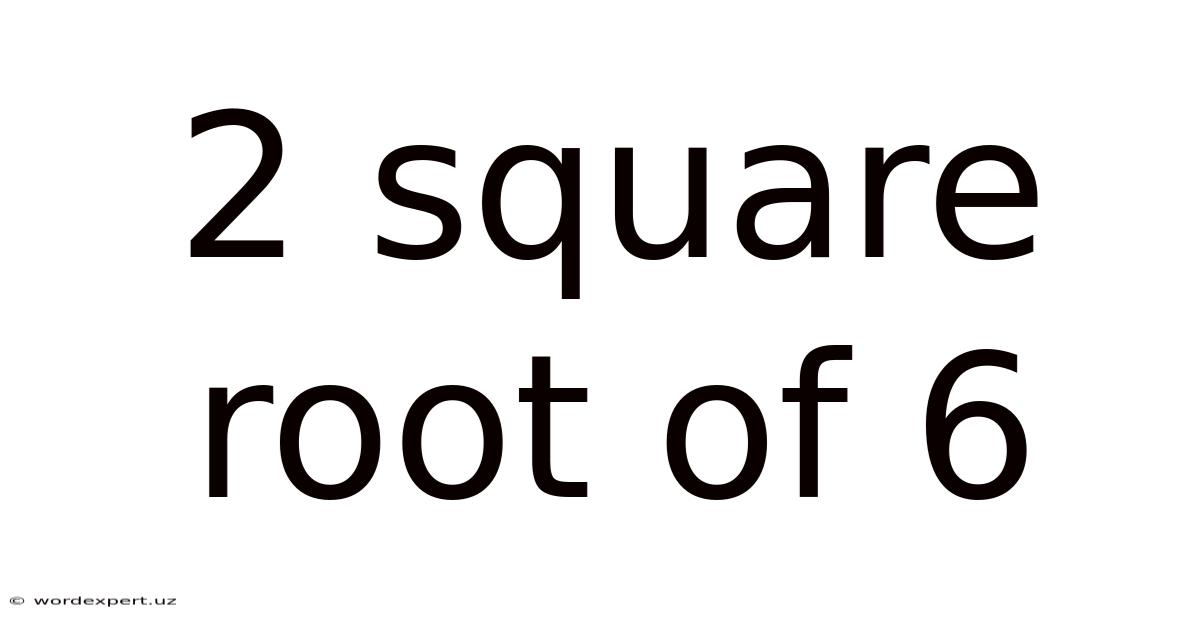
Table of Contents
Unveiling the Mysteries of 2√6: A Deep Dive into Irrational Numbers
Understanding the square root of a number, and specifically 2√6, is fundamental to grasping core concepts in mathematics. This article will explore 2√6, not just as a simple mathematical expression, but as a gateway to understanding irrational numbers, their properties, and their practical applications. We’ll delve into its calculation, its representation on a number line, its relationship to other mathematical concepts, and finally, answer frequently asked questions to solidify your understanding.
What is 2√6? A Primer on Square Roots and Irrational Numbers
At its simplest, 2√6 represents two times the square root of six. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. However, not all numbers have whole number square roots. This leads us to the concept of irrational numbers.
Irrational numbers are numbers that cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representation goes on forever without repeating. π (pi) and e (Euler's number) are famous examples. √6 is also an irrational number because there's no fraction that, when multiplied by itself, equals 6. Its decimal approximation is approximately 2.449. Therefore, 2√6 is approximately 2 * 2.449 = 4.898. This approximation is useful for practical calculations, but it's crucial to remember that it's not the exact value.
Calculating 2√6: Methods and Approximations
While we can't find an exact decimal representation for √6, we can use several methods to approximate its value, and subsequently, the value of 2√6:
-
Using a Calculator: The most straightforward method is using a calculator with a square root function. Simply enter √6 and then multiply the result by 2. This provides a highly accurate approximation.
-
Babylonian Method (or Heron's Method): This iterative method refines an initial guess to progressively closer approximations of the square root. Let's illustrate:
- Make an initial guess: Let's guess 2.5.
- Improve the guess: Divide 6 by your guess (6/2.5 = 2.4).
- Average: Average your guess and the result from step 2: (2.5 + 2.4)/2 = 2.45.
- Repeat: Use 2.45 as your new guess and repeat steps 2 and 3. The more you repeat this process, the closer your approximation gets to the actual value of √6.
-
Series Expansion: More advanced mathematical methods involve using Taylor series or other series expansions to approximate the square root. These methods are more complex and typically require knowledge of calculus.
Regardless of the method used, remember that any calculated value of 2√6 will be an approximation. The true value remains an irrational number with an infinitely long, non-repeating decimal representation.
Representing 2√6 on the Number Line
Visualizing 2√6 on a number line helps solidify its position within the number system. Since it's between 4 and 5 (as 2√6 ≈ 4.898), we can locate it more precisely using a geometrical approach:
-
Construct a right-angled triangle: Draw a right-angled triangle with legs of length 2 and √6. The hypotenuse of this triangle will have a length of approximately 2√6 using the Pythagorean theorem (a² + b² = c²).
-
Estimate √6: You can estimate √6 geometrically by constructing a square with an area of 6 square units. The length of the side of this square will be approximately √6.
-
Transfer the length: Using a compass, transfer the length of the hypotenuse (or the estimated length of √6 multiplied by 2) onto the number line, starting from zero. The point where the length ends marks the approximate location of 2√6.
This geometrical approach provides a visual understanding of the number's approximate value and its relationship to other numbers on the number line.
2√6 in Different Mathematical Contexts
2√6 isn't just an isolated number; it appears in various mathematical contexts:
-
Geometry: As shown in the number line representation, it can be used to represent lengths and distances in geometric problems, particularly those involving the Pythagorean theorem or similar geometric constructions.
-
Algebra: It can appear as a solution to quadratic equations or more complex algebraic expressions.
-
Trigonometry: It might be found in calculations involving angles and trigonometric functions, although this isn't as common as its appearance in geometry and algebra.
-
Calculus: Although not directly, its components (√6 and the number 2) appear in different calculus applications like differentiation and integration, particularly in problems dealing with areas and volumes.
The Significance of Irrational Numbers
Understanding 2√6 contributes significantly to a broader understanding of irrational numbers. These numbers, despite their seemingly unusual nature, are essential building blocks of mathematics and have significant implications:
-
Expanding Number Systems: Irrational numbers dramatically expand the number system beyond rational numbers, providing a much richer and more complete mathematical framework.
-
Precision and Accuracy: While approximations are often used in practical applications, the concept of irrational numbers highlights the inherent limitations of representing certain numbers precisely using decimals or fractions.
-
Mathematical Modeling: Irrational numbers play a critical role in various mathematical models used across diverse fields like physics, engineering, and computer science. For example, π is fundamental to the calculation of circles' circumference and areas, while e is crucial in exponential growth and decay models.
Frequently Asked Questions (FAQ)
Q: Can 2√6 be simplified further?
A: No, 2√6 is already in its simplest form. While 6 can be factored (2 x 3), there are no perfect square factors within 6, preventing further simplification of the square root.
Q: What is the difference between √12 and 2√6?
A: √12 can be simplified because it contains a perfect square factor. √12 = √(4 x 3) = 2√3. Therefore, √12 and 2√6 are not equal. They are different irrational numbers.
Q: How can I use 2√6 in real-world problems?
A: In real-world scenarios, you would typically use an approximation of 2√6. For example, if you're calculating the diagonal of a rectangle with sides of length a and b, and a² + b² = 24, then the diagonal would be √24 = 2√6. You would substitute an approximate value like 4.898 to get a practical result.
Q: Is it possible to represent 2√6 as a repeating decimal?
A: No. By definition, irrational numbers cannot be represented as repeating decimals. Their decimal representation continues infinitely without any repeating pattern.
Conclusion: Embracing the Irrational
2√6, while seemingly a simple mathematical expression, provides a valuable entry point into the fascinating world of irrational numbers. Understanding its calculation, its representation, and its place within the broader mathematical landscape enhances your appreciation of the beauty and complexity of the number system. Remember, embracing the irrational allows for a deeper understanding of mathematical principles and their application in various fields. While we can only approximate its value, the theoretical significance of 2√6 and numbers like it remains profound and essential to mathematical understanding.
Latest Posts
Latest Posts
-
Miles To Engine Hours Conversion
Sep 22, 2025
-
60 Days From May 7
Sep 22, 2025
-
Hair Growth Month By Month
Sep 22, 2025
-
How Many Tablespoons Is 60ml
Sep 22, 2025
-
30 Days From March 21
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 Square Root Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.