25 Percent Off Of 50
wordexpert
Sep 13, 2025 · 5 min read
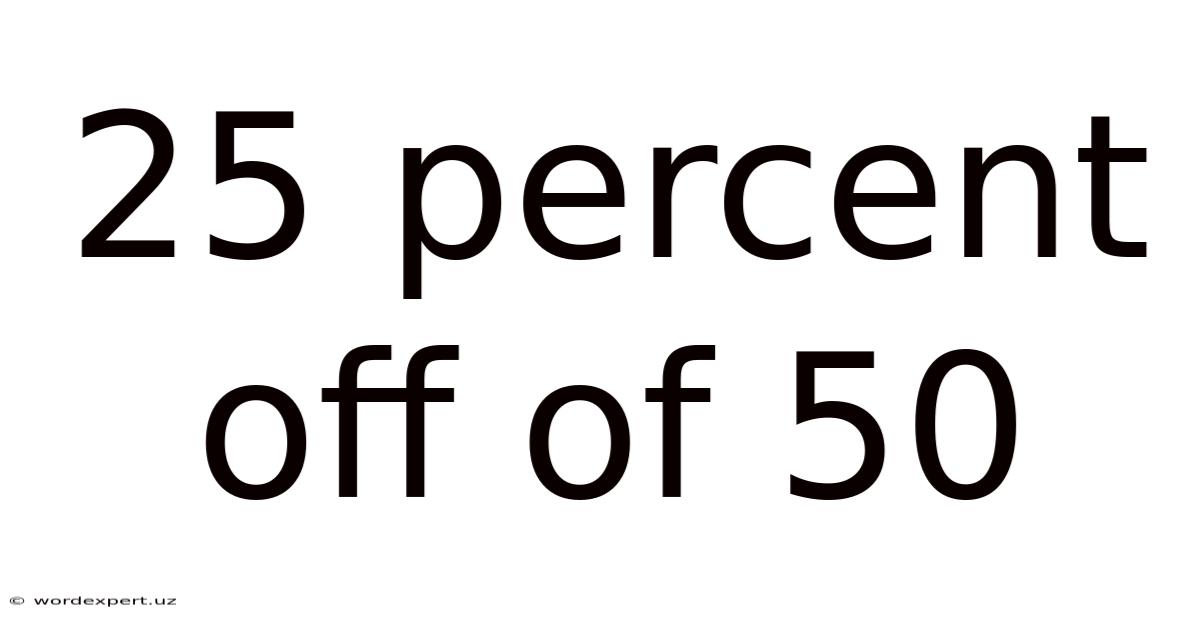
Table of Contents
25 Percent Off of 50: A Comprehensive Guide to Percentage Calculations
Calculating discounts is a fundamental skill applicable in various aspects of life, from shopping and budgeting to understanding financial reports and sales. This comprehensive guide will delve deep into calculating 25% off of 50, explaining the process step-by-step, exploring different methods, and providing insights into the underlying mathematical principles. We'll also address common misconceptions and offer practical applications to solidify your understanding. This guide is designed for everyone, from those new to percentage calculations to those seeking a more in-depth understanding.
Understanding Percentages
Before we tackle the specific problem of calculating 25% off of 50, let's establish a firm grasp on the concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol % denotes "per cent" or "out of 100." For example, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Understanding this fundamental relationship is crucial for all percentage calculations.
Method 1: The Fraction Method
This method utilizes the fraction equivalent of a percentage. Since 25% is equivalent to 1/4, we can calculate 25% of 50 by multiplying 50 by 1/4:
50 * (1/4) = 50/4 = 12.5
This tells us that 25% of 50 is 12.5. To find the final price after a 25% discount, we subtract this value from the original price:
50 - 12.5 = 37.5
Therefore, 25% off of 50 is $\boxed{37.5}$.
Method 2: The Decimal Method
This method converts the percentage to a decimal before performing the calculation. To convert a percentage to a decimal, divide the percentage by 100. For 25%, this would be:
25 / 100 = 0.25
Now, we multiply the original price (50) by the decimal equivalent of the percentage (0.25):
50 * 0.25 = 12.5
This gives us the amount of the discount, which is 12.5. Subtracting this from the original price gives us the final price:
50 - 12.5 = 37.5
Again, 25% off of 50 is $\boxed{37.5}$.
Method 3: Using Proportions
This method leverages the concept of proportions to solve the problem. We can set up a proportion to represent the relationship between the percentage and the amount:
25/100 = x/50
Where 'x' represents the amount of the discount. To solve for 'x', we cross-multiply:
25 * 50 = 100 * x
1250 = 100x
x = 1250 / 100
x = 12.5
This confirms that the discount amount is 12.5. Subtracting this from the original price gives us the final price of 37.5.
Method 4: The Percentage Decrease Formula
A more direct approach involves using the percentage decrease formula:
Final Price = Original Price * (1 - Percentage Decrease)
In this case:
Final Price = 50 * (1 - 0.25)
Final Price = 50 * 0.75
Final Price = 37.5
This formula directly calculates the final price after the discount, eliminating the need for a separate subtraction step.
Understanding the Calculation in Context
The calculation "25% off of 50" implies a reduction of 25% from an initial value of 50. This scenario frequently arises in retail sales, where discounts are commonly expressed as percentages. For example, a $50 item discounted by 25% would cost $37.50 after the discount. The same principle applies to various other contexts involving percentage reductions, such as calculating sale prices, interest rates, or tax deductions.
Practical Applications and Examples
The ability to quickly calculate percentage discounts is invaluable in everyday life. Here are a few practical examples:
- Shopping: When comparing prices and finding the best deals, understanding percentage discounts is crucial. You can easily determine which offer is more advantageous.
- Budgeting: Calculating discounts helps you stay within your budget by accurately determining the final cost of items before making a purchase.
- Investing: Understanding percentage changes in investment values is essential for tracking portfolio performance and making informed investment decisions.
- Sales and Finance: In business settings, accurately calculating percentages is fundamental for analyzing sales figures, profit margins, and financial statements.
Common Misconceptions about Percentage Calculations
Several common misconceptions can lead to errors in percentage calculations. Let's address some of them:
- Adding percentages directly: Adding percentages directly (e.g., 25% + 50% = 75%) is incorrect unless the percentages are applied to the same base value. If a 25% discount is followed by a 50% discount, the calculations must be performed sequentially.
- Confusing percentage increase and decrease: Remember that calculating a percentage increase involves adding the calculated percentage to the original value, while a percentage decrease involves subtracting it.
- Incorrect decimal conversion: Errors often arise when converting percentages to decimals. Always remember to divide the percentage by 100.
Frequently Asked Questions (FAQ)
Q: What is the best method for calculating percentage discounts?
A: The best method depends on your comfort level with different mathematical approaches. The decimal method is generally efficient and straightforward, while the percentage decrease formula offers a more direct calculation of the final price.
Q: Can I use a calculator to solve these problems?
A: Yes, calculators are incredibly helpful for percentage calculations, especially when dealing with more complex problems. Most calculators have a percentage function (%) that simplifies the process.
Q: What if the percentage discount is not a whole number (e.g., 27.5%)?
A: The same methods apply. Simply convert the percentage to a decimal (27.5% = 0.275) and proceed with the calculation as described above.
Q: How can I improve my understanding of percentages?
A: Practice is key. Regularly work through percentage problems using different methods. You can find numerous practice exercises online or in textbooks.
Q: What if I need to calculate multiple discounts sequentially?
A: For sequential discounts, apply the discounts one after the other. Do not add the percentages. For example, a 25% discount followed by a 10% discount on the resulting price would require two separate calculations.
Conclusion
Calculating 25% off of 50, resulting in a final price of 37.5, is a fundamental application of percentage calculations. Understanding the different methods presented in this guide—the fraction method, the decimal method, the proportions method, and the percentage decrease formula—empowers you to solve various percentage-related problems confidently and accurately. Mastering this skill enhances your ability to manage finances, make informed purchasing decisions, and analyze data effectively in various real-world scenarios. Remember that consistent practice and understanding the underlying mathematical principles are key to becoming proficient in percentage calculations. Continue practicing, and you’ll find that these calculations become second nature.
Latest Posts
Latest Posts
-
3 000 Mcg To Iu
Sep 13, 2025
-
Slant Height Of Pyramid Calculator
Sep 13, 2025
-
Convert Moles To Grams Calculator
Sep 13, 2025
-
Dc Voltage Wire Size Chart
Sep 13, 2025
-
50 Oz How Many Pounds
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 25 Percent Off Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.