4 1/8 As A Decimal
wordexpert
Sep 24, 2025 · 5 min read
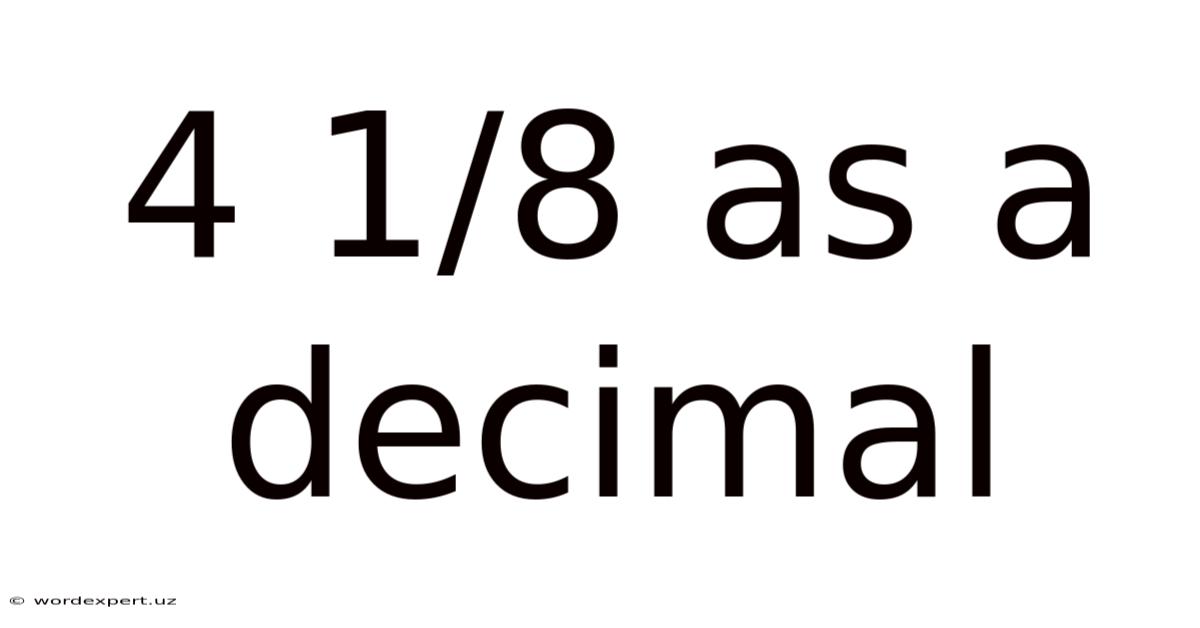
Table of Contents
Decoding 4 1/8 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 4 1/8 into its decimal equivalent, explaining the underlying principles and providing practical applications. We'll delve into the different methods, address common misconceptions, and even explore the connection to real-world scenarios. By the end, you'll not only know the answer but also understand why the answer is what it is.
Understanding Mixed Numbers and Fractions
Before we dive into the conversion, let's clarify some key terms. A mixed number combines a whole number and a fraction, such as 4 1/8. The whole number (4 in this case) represents a complete unit, while the fraction (1/8) represents a part of a unit. A fraction, in its simplest form, is a representation of a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). In 1/8, 1 is the numerator and 8 is the denominator.
Method 1: Converting the Fraction to a Decimal
The most straightforward approach to converting 4 1/8 to a decimal involves first converting the fraction 1/8 to a decimal. We can do this by performing a simple division:
1 ÷ 8 = 0.125
Therefore, 1/8 is equivalent to 0.125.
Now, we simply add the whole number back into the equation:
4 + 0.125 = 4.125
Therefore, 4 1/8 as a decimal is 4.125.
Method 2: Converting the Mixed Number Directly
Alternatively, we can convert the entire mixed number directly. We first convert the mixed number into an improper fraction. To do this, we multiply the whole number by the denominator and add the numerator:
(4 * 8) + 1 = 33
This becomes the new numerator, while the denominator remains the same:
33/8
Now, we divide the numerator by the denominator:
33 ÷ 8 = 4.125
Again, we arrive at the same answer: 4.125
Understanding the Decimal Place Value
The decimal number 4.125 can be broken down into its place values:
- 4: Represents four ones (or units).
- 1: Represents one tenth (0.1).
- 2: Represents two hundredths (0.02).
- 5: Represents five thousandths (0.005).
Understanding place value is crucial for comprehending the magnitude of each digit in a decimal number.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals has widespread applications in various fields:
- Finance: Calculating interest rates, discounts, and profit margins often involves working with both fractions and decimals.
- Engineering: Precise measurements and calculations in engineering require accurate decimal representations.
- Science: Data analysis and scientific calculations often rely on decimal representations for accuracy.
- Cooking and Baking: Recipe adjustments frequently involve converting fractions to decimals for precise measurements.
- Everyday Life: Sharing information involving parts of a whole, such as splitting a bill or measuring ingredients, is simpler with decimals.
Common Mistakes to Avoid
While the conversion process is relatively simple, several common mistakes can lead to inaccurate results:
- Incorrect Division: Ensuring the correct order of operations when dividing the numerator by the denominator is crucial.
- Ignoring the Whole Number: Remember to add the whole number back after converting the fraction to a decimal.
- Decimal Point Placement: Pay close attention to the placement of the decimal point in the final answer.
Expanding the Understanding: Working with Different Fractions
Let's explore how this process applies to other fractions to further solidify your understanding. Consider the following examples:
- 2 3/4: First, convert 3/4 to a decimal (3 ÷ 4 = 0.75). Then add the whole number: 2 + 0.75 = 2.75
- 1 1/2: Convert 1/2 to a decimal (1 ÷ 2 = 0.5). Then add the whole number: 1 + 0.5 = 1.5
- 5 1/16: Convert 1/16 to a decimal (1 ÷ 16 = 0.0625). Then add the whole number: 5 + 0.0625 = 5.0625
These examples demonstrate the consistent application of the conversion method regardless of the specific fraction involved.
Advanced Concepts: Recurring Decimals
While many fractions convert to terminating decimals (like 4.125), some result in recurring decimals. A recurring decimal is a decimal that has a repeating sequence of digits. For instance, 1/3 converts to 0.3333... (the 3 repeats infinitely). Understanding how to represent these recurring decimals accurately is a more advanced topic. However, the fundamental principle of division remains the same.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 4 1/8 to a decimal?
A: Absolutely! Most calculators have a fraction-to-decimal conversion function. Simply input the fraction (or the mixed number) and the calculator will provide the decimal equivalent.
Q: Why is it important to understand fraction-to-decimal conversions?
A: This skill is essential for numerous applications across various fields, improving accuracy and efficiency in calculations.
Q: What if the fraction has a larger denominator?
A: The process remains the same. You simply divide the numerator by the denominator to obtain the decimal equivalent. The calculation might be more complex, but the principle is consistent.
Q: Are there other methods to convert fractions to decimals?
A: Yes, while division is the most common method, other techniques exist, especially for simpler fractions. For instance, you can memorize the decimal equivalents of common fractions like 1/2 (0.5), 1/4 (0.25), and 1/8 (0.125).
Conclusion: Mastering Decimal Conversions
Converting 4 1/8 to a decimal, resulting in 4.125, highlights the fundamental importance of understanding fraction-to-decimal conversions. This skill transcends simple arithmetic and is a critical building block for success in various academic and professional pursuits. By mastering this skill and understanding the underlying principles, you equip yourself with a valuable tool for tackling more complex mathematical problems and real-world applications. Remember to practice regularly and utilize different methods to solidify your understanding. With consistent effort, you'll confidently navigate the world of fractions and decimals.
Latest Posts
Latest Posts
-
How Much Longer Till 1 39
Sep 24, 2025
-
What Is 10 Of 50
Sep 24, 2025
-
100 000 Milliseconds To Seconds
Sep 24, 2025
-
Cuanto Son Libras En Kilos
Sep 24, 2025
-
Cuantos Mililitros Son 2 Oz
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 4 1/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.