What Is 10 Of $50
wordexpert
Sep 24, 2025 · 5 min read
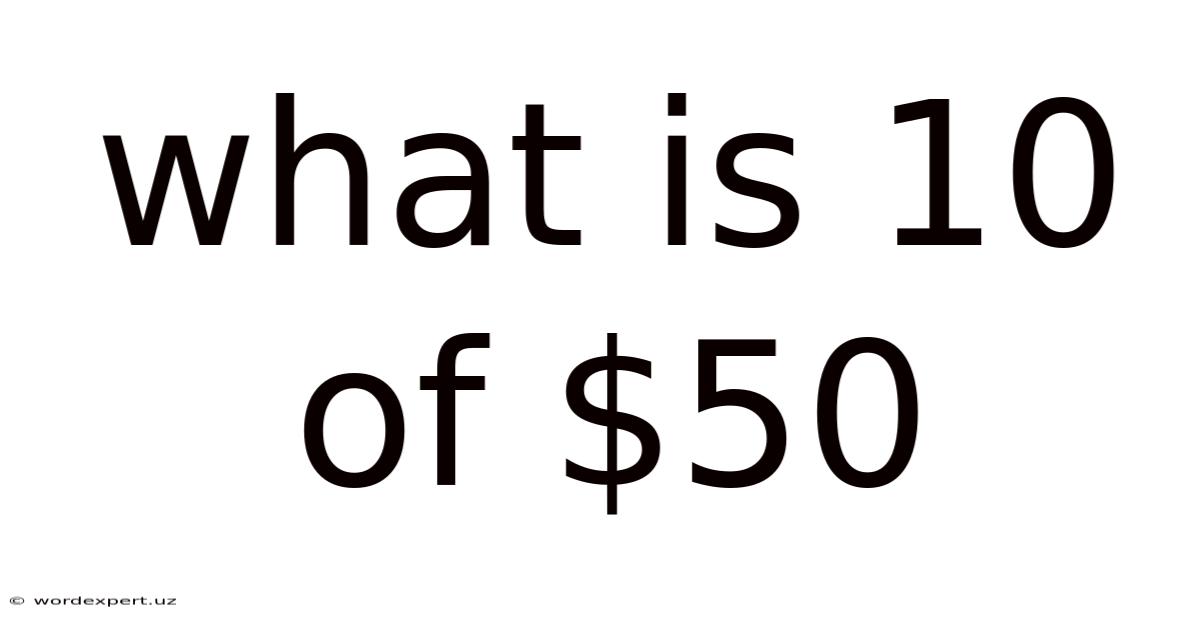
Table of Contents
What is 10% of $50? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to understanding financial reports and statistics. This article will delve into the seemingly simple question, "What is 10% of $50?", but it will go far beyond just providing the answer. We'll explore the underlying concepts of percentage calculations, different methods for solving these problems, and even extend our understanding to more complex scenarios. This guide is designed for everyone, from students grappling with basic math to adults looking to refresh their skills or deepen their understanding of percentages.
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a part of 100. The word "percent" literally means "out of one hundred" ("per centum" in Latin). So, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10. This fundamental understanding is key to solving any percentage problem.
Method 1: Using the Decimal Equivalent
The most straightforward method for calculating 10% of $50 involves converting the percentage to its decimal equivalent. As mentioned earlier, 10% is equal to 0.10. To find 10% of $50, we simply multiply $50 by 0.10:
$50 * 0.10 = $5
Therefore, 10% of $50 is $\boxed{$5}$.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 10% can be written as 10/100, which simplifies to 1/10. To find 10% of $50 using this method, we multiply $50 by the fraction 1/10:
$50 * (1/10) = $50/10 = $5
This method demonstrates the equivalence between percentages, decimals, and fractions – all valuable tools in your mathematical arsenal.
Method 3: The Proportion Method
The proportion method provides a more visual and intuitive way to solve percentage problems. We can set up a proportion to represent the problem:
10/100 = x/50
Here, 'x' represents the unknown value (10% of $50). To solve for 'x', we cross-multiply:
10 * 50 = 100 * x
500 = 100x
x = 500/100
x = 5
Again, we find that 10% of $50 is $\boxed{$5}$. This method is particularly helpful when dealing with more complex percentage problems.
Extending the Concept: Calculating Other Percentages of $50
Now that we've mastered calculating 10% of $50, let's explore how to calculate other percentages of the same amount. The principles remain the same; we can use any of the three methods discussed above.
- 20% of $50: Using the decimal method: $50 * 0.20 = $10
- 25% of $50: Using the fraction method: $50 * (1/4) = $12.50
- 50% of $50: This is half of $50: $50 * 0.50 = $25
- 75% of $50: Three-quarters of $50: $50 * 0.75 = $37.50
- 100% of $50: The entire amount: $50 * 1.00 = $50
Real-World Applications: Percentages in Everyday Life
Understanding percentage calculations is crucial for navigating many everyday situations:
- Shopping: Calculating discounts (e.g., a 20% off sale), sales tax, or tips at restaurants.
- Finance: Understanding interest rates on loans or savings accounts, calculating investment returns, or analyzing financial statements.
- Science: Expressing data as percentages in scientific reports and experiments.
- Education: Calculating grades based on percentages, understanding test scores, and analyzing statistical data.
Beyond the Basics: More Complex Percentage Problems
While calculating 10% of $50 is relatively straightforward, percentage problems can become more complex. Here are a few examples:
- Finding the percentage increase or decrease: If the price of an item increases from $50 to $60, what is the percentage increase?
- Calculating a percentage of a percentage: What is 20% of 15% of $50?
- Finding the original value after a percentage change: An item is on sale for $40 after a 20% discount. What was the original price?
Solving these more advanced problems requires a deeper understanding of percentage concepts and algebraic techniques.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate percentages?
A: The easiest method often depends on the specific problem and your personal preference. The decimal method is generally quick and efficient for many scenarios. However, the fraction method can be helpful when dealing with easily convertible fractions (like 25%, 50%, 75%).
Q: How can I improve my skills in calculating percentages?
A: Practice is key! Solve various percentage problems, starting with simple ones and gradually increasing the complexity. You can find practice problems online or in textbooks. Understanding the different methods (decimal, fraction, proportion) will provide you with flexibility in tackling different types of problems.
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, many online percentage calculators are available. These can be helpful for checking your work or solving more complex problems quickly. However, it's important to understand the underlying principles to effectively utilize these tools and to solve problems independently.
Q: Why are percentages so important?
A: Percentages are a universal language for representing proportions and ratios. Their widespread use across various fields means understanding them is essential for effective communication, problem-solving, and critical thinking.
Conclusion
Calculating 10% of $50, while seemingly simple, serves as a gateway to understanding a broader concept – the power of percentages. Mastering percentage calculations equips you with a valuable skill applicable across diverse fields, enabling you to analyze data, make informed decisions, and confidently navigate the numerical aspects of everyday life. By understanding the different methods and practicing regularly, you can build confidence and proficiency in this essential mathematical skill. Remember, the journey from understanding the basics of "What is 10% of $50?" to confidently tackling complex percentage problems is achievable through consistent effort and practice.
Latest Posts
Latest Posts
-
How Long Is 139 Hours
Sep 24, 2025
-
Half An Ounce In Ml
Sep 24, 2025
-
Sales Tax In Thousand Oaks
Sep 24, 2025
-
What Is 15 Of 150
Sep 24, 2025
-
Area Of A Pipe Calculator
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of $50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.