5 Divided By 4 5
wordexpert
Sep 25, 2025 · 5 min read
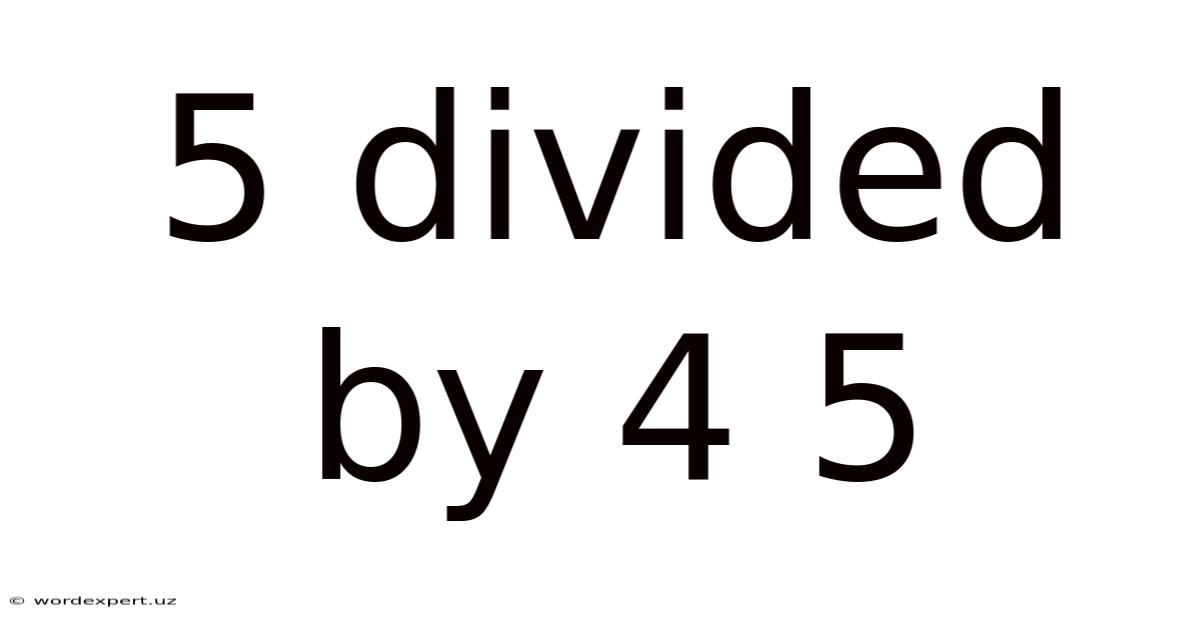
Table of Contents
Decoding 5 Divided by 45: A Deep Dive into Division
Many find division a straightforward operation, especially with simple whole numbers. However, the seemingly simple problem of "5 divided by 45" (or 5/45) presents an opportunity to explore deeper mathematical concepts and solidify our understanding of fractions, decimals, and their real-world applications. This article will unravel this seemingly simple division problem, examining its solution, exploring its underlying principles, and demonstrating its relevance in various contexts.
Understanding the Problem: 5 ÷ 45
At its core, 5 ÷ 45 asks: "How many times does 45 fit into 5?" Intuitively, we know 45 is larger than 5, meaning 45 cannot fit into 5 even once. This leads us to the realm of fractions and decimals, where the answer isn't a whole number but a fraction or a decimal representing a part of a whole.
Step-by-Step Solution: From Fraction to Decimal
-
Expressing as a Fraction: The division problem 5 ÷ 45 can be equivalently represented as the fraction 5/45.
-
Simplifying the Fraction: To understand the fraction better, we simplify it by finding the greatest common divisor (GCD) of the numerator (5) and the denominator (45). The GCD of 5 and 45 is 5. Dividing both the numerator and the denominator by 5, we get:
5/45 = (5 ÷ 5) / (45 ÷ 5) = 1/9
-
Converting to a Decimal: The simplified fraction 1/9 represents one-ninth. To convert this fraction to a decimal, we perform the division: 1 ÷ 9. This division results in a repeating decimal:
1 ÷ 9 = 0.111111...
We can represent this repeating decimal using a bar over the repeating digit: 0.̅1
Therefore, 5 divided by 45 is equal to 1/9, which is approximately 0.111.
The Mathematical Underpinnings: Fractions and Decimals
This problem highlights the fundamental relationship between fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers (numerator and denominator). A decimal is another way to represent a fraction, where the denominator is a power of 10 (e.g., 10, 100, 1000).
The process of converting a fraction to a decimal involves dividing the numerator by the denominator. Sometimes, this division results in a terminating decimal (e.g., 1/4 = 0.25), and sometimes it results in a repeating decimal (e.g., 1/9 = 0.̅1), as seen in our example. Repeating decimals are represented using a bar above the repeating digits to indicate the pattern.
Real-World Applications: Where Does This Matter?
While seemingly abstract, understanding division problems like 5/45 has practical applications in various fields:
-
Baking and Cooking: Recipes often require precise measurements. If a recipe calls for 45 grams of flour, but you only have 5 grams, understanding the fraction 5/45 (or 1/9) allows you to scale down the recipe proportionally.
-
Finance and Budgeting: Calculating percentages or proportions of budgets often involves division. If your monthly budget is $45 and you spend $5 on entertainment, you’ve spent 5/45 (or 1/9) of your budget on entertainment.
-
Engineering and Construction: Scaling down blueprints or calculating material quantities involves proportional reasoning, often requiring division of fractions or decimals.
-
Data Analysis: When working with datasets, you might need to calculate percentages or proportions of different categories or groups. Understanding fraction to decimal conversion is essential for data representation and interpretation.
-
Everyday Life: Dividing a pizza among friends, sharing candy, or portioning ingredients are all real-life scenarios that rely on fractional and decimal understanding.
Beyond the Basics: Exploring Further Mathematical Concepts
This simple division problem opens the door to exploring more advanced mathematical ideas:
-
Rational Numbers: The result 1/9 is a rational number, a number that can be expressed as a fraction of two integers. All terminating and repeating decimals are rational numbers.
-
Irrational Numbers: In contrast to rational numbers, irrational numbers cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating (e.g., π, √2).
-
Limits and Series: The repeating decimal 0.̅1 can be expressed as an infinite geometric series: 1/10 + 1/100 + 1/1000 + ... Understanding infinite series is crucial in calculus and advanced mathematics.
Frequently Asked Questions (FAQ)
-
Q: Can I leave the answer as 1/9? A: Yes, 1/9 is a perfectly valid and often preferred answer, as it represents the exact value. 0.111... is an approximation.
-
Q: Why does 1/9 result in a repeating decimal? A: Because when you perform long division, the remainder never becomes zero. The division process continues indefinitely, creating a repeating pattern.
-
Q: Are there other ways to solve 5 ÷ 45? A: Yes, you could use a calculator, but understanding the manual process of fraction simplification and decimal conversion is important for building a strong foundation in mathematics.
-
Q: What if the numbers were larger? A: The same principles apply, regardless of the size of the numbers. You would follow the same steps: express as a fraction, simplify, and convert to a decimal if needed.
Conclusion: The Power of Understanding Division
The seemingly simple problem of 5 divided by 45 offers a rich learning opportunity. It reinforces our understanding of fractions, decimals, rational numbers, and their interconnectedness. Furthermore, it demonstrates the practical relevance of these mathematical concepts in various real-world scenarios. By mastering these foundational concepts, we equip ourselves with essential tools for problem-solving and critical thinking across multiple disciplines. The journey from a simple division problem to a deeper understanding of mathematical principles highlights the power of exploration and the beauty of mathematical connections. So, the next time you encounter a similar problem, remember the journey from 5/45 to 1/9 to 0.̅1, and the numerous applications this simple calculation encompasses.
Latest Posts
Latest Posts
-
67 Out Of 100 Grade
Sep 25, 2025
-
What Is 25 Percent Of
Sep 25, 2025
-
Convert I To Polar Form
Sep 25, 2025
-
10ml Equals How Many Teaspoons
Sep 25, 2025
-
Draperies For 9 Foot Ceilings
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.