5 Percent Of 30 000
wordexpert
Sep 17, 2025 · 5 min read
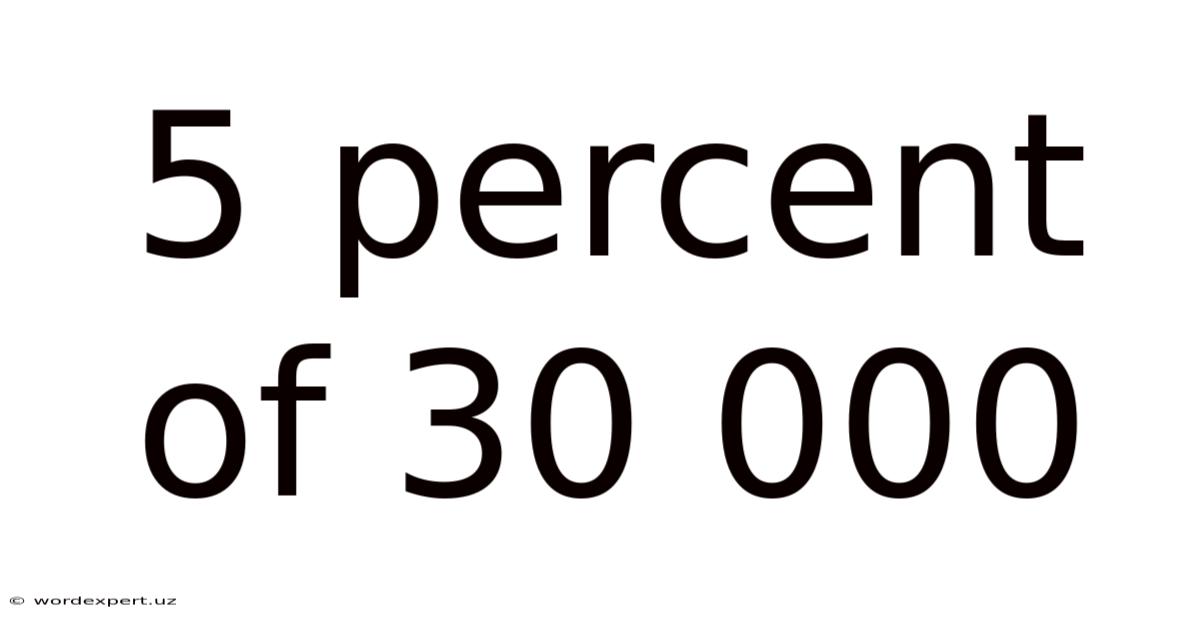
Table of Contents
Decoding 5 Percent of 30,000: A Comprehensive Guide to Percentage Calculations
Finding 5 percent of 30,000 might seem like a simple arithmetic problem, but understanding the underlying principles of percentage calculations is crucial for various applications in everyday life, from budgeting and finance to sales and discounts. This comprehensive guide will not only show you how to calculate 5% of 30,000 but also delve deeper into the concept of percentages, offering various methods and practical examples to solidify your understanding. This article covers different approaches, including using fractions, decimals, and even mental math techniques, to help you master percentage calculations.
Understanding Percentages: A Foundation
Before diving into the calculation, let's establish a clear understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 5% means 5 out of 100, which can be written as the fraction 5/100 or the decimal 0.05.
This fundamental understanding is vital because it allows us to translate percentage problems into equivalent fraction or decimal problems, making the calculation much easier.
Method 1: The Decimal Method
This is arguably the most straightforward and commonly used method for calculating percentages. It involves converting the percentage to its decimal equivalent and then multiplying it by the original number.
Steps:
-
Convert the percentage to a decimal: To convert 5% to a decimal, divide it by 100: 5% / 100 = 0.05
-
Multiply the decimal by the original number: Multiply 0.05 by 30,000: 0.05 * 30,000 = 1500
Therefore, 5% of 30,000 is 1500.
Method 2: The Fraction Method
This method utilizes the fractional representation of the percentage. It's particularly helpful for understanding the underlying relationship between the percentage and the whole.
Steps:
-
Express the percentage as a fraction: 5% can be written as the fraction 5/100.
-
Simplify the fraction (optional): The fraction 5/100 can be simplified to 1/20.
-
Multiply the fraction by the original number: Multiply 1/20 by 30,000: (1/20) * 30,000 = 1500
Again, we arrive at the answer: 5% of 30,000 is 1500.
Method 3: Using Proportions
This method is a more formal approach, particularly useful when dealing with more complex percentage problems. It involves setting up a proportion and solving for the unknown value.
Steps:
-
Set up a proportion: We can set up a proportion as follows:
x / 30,000 = 5 / 100
Where 'x' represents the unknown value (5% of 30,000).
-
Cross-multiply: Cross-multiplying gives us:
100x = 5 * 30,000
100x = 150,000
-
Solve for x: Divide both sides by 100:
x = 150,000 / 100
x = 1500
Once again, the result is 1500. 5% of 30,000 is 1500.
Method 4: Mental Math Techniques (for simpler percentages)
For simple percentages like 5%, 10%, 25%, and 50%, mental math techniques can be employed for quicker calculations.
-
Finding 10%: Finding 10% of a number is simply dividing the number by 10. 10% of 30,000 is 30,000 / 10 = 3000.
-
Finding 5%: Since 5% is half of 10%, we can find 5% by dividing 10% by 2. Therefore, 5% of 30,000 is 3000 / 2 = 1500.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios:
-
Finance: Calculating interest on loans, savings accounts, and investments. Determining the percentage increase or decrease in stock prices. Analyzing financial statements and reports.
-
Sales and Discounts: Calculating discounts offered on products or services. Determining the final price after applying a discount. Analyzing sales figures and revenue growth.
-
Taxes: Calculating sales tax, income tax, and property tax. Understanding tax brackets and tax rates.
-
Statistics: Interpreting statistical data that uses percentages to represent proportions and trends. Analyzing survey results and demographic data.
-
Everyday Budgeting: Allocating a certain percentage of income towards different expenses (e.g., housing, food, transportation). Tracking spending habits and managing personal finances effectively.
Beyond the Basics: More Complex Percentage Problems
While the example of 5% of 30,000 is relatively straightforward, the principles discussed here can be applied to more complex scenarios. For instance:
-
Finding the percentage increase or decrease: Imagine a product's price increased from 20,000 to 22,000. To find the percentage increase, you would first calculate the difference (22,000 - 20,000 = 2000), then divide the difference by the original price (2000 / 20,000 = 0.1), and finally multiply by 100 to express it as a percentage (0.1 * 100 = 10%). The price increased by 10%.
-
Finding the original value after a percentage change: If a product is discounted by 20% and the final price is 16,000, we can work backward to find the original price. Let 'x' be the original price. Then, 0.8x = 16,000 (since a 20% discount means 80% remains). Solving for x gives us x = 20,000.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a more complex percentage, like 17.5% of 30,000?
A: You would apply the same decimal method. Convert 17.5% to a decimal (0.175) and multiply it by 30,000. This would give you 5250.
Q2: Are there any online calculators or tools that can help with percentage calculations?
A: Yes, many online calculators are available to assist with percentage calculations. Simply search for "percentage calculator" on your preferred search engine.
Q3: Why is understanding percentages important in everyday life?
A: Percentages are a fundamental part of daily life, from understanding discounts and sales to managing finances and interpreting data. They are essential for making informed decisions and navigating the numerical world around us.
Q4: Can I use a spreadsheet program like Microsoft Excel to calculate percentages?
A: Absolutely! Spreadsheet programs offer powerful tools for percentage calculations. You can use simple formulas to calculate percentages, and even create more complex models for financial planning and analysis.
Conclusion
Calculating 5% of 30,000, and understanding percentage calculations in general, is a foundational skill with wide-ranging applications. By mastering the different methods outlined above – the decimal method, the fraction method, the proportion method, and even mental math techniques for simpler calculations – you equip yourself with a powerful tool for navigating various aspects of life, from personal finance to professional analysis. Remember that the key is to understand the underlying principles, and the specific method you choose will often depend on the complexity of the problem and your personal preference. Practice makes perfect, so don't hesitate to work through various examples to solidify your understanding and build confidence in your percentage calculation skills.
Latest Posts
Latest Posts
-
How Long Is 57 Months
Sep 17, 2025
-
3 Percent Of 200 000
Sep 17, 2025
-
90 Days From September 17
Sep 17, 2025
-
Weight Of Steel Pipe Calculator
Sep 17, 2025
-
How To Measure Your Stride
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 5 Percent Of 30 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.