Percent Of 4 Is 7
wordexpert
Sep 22, 2025 · 5 min read
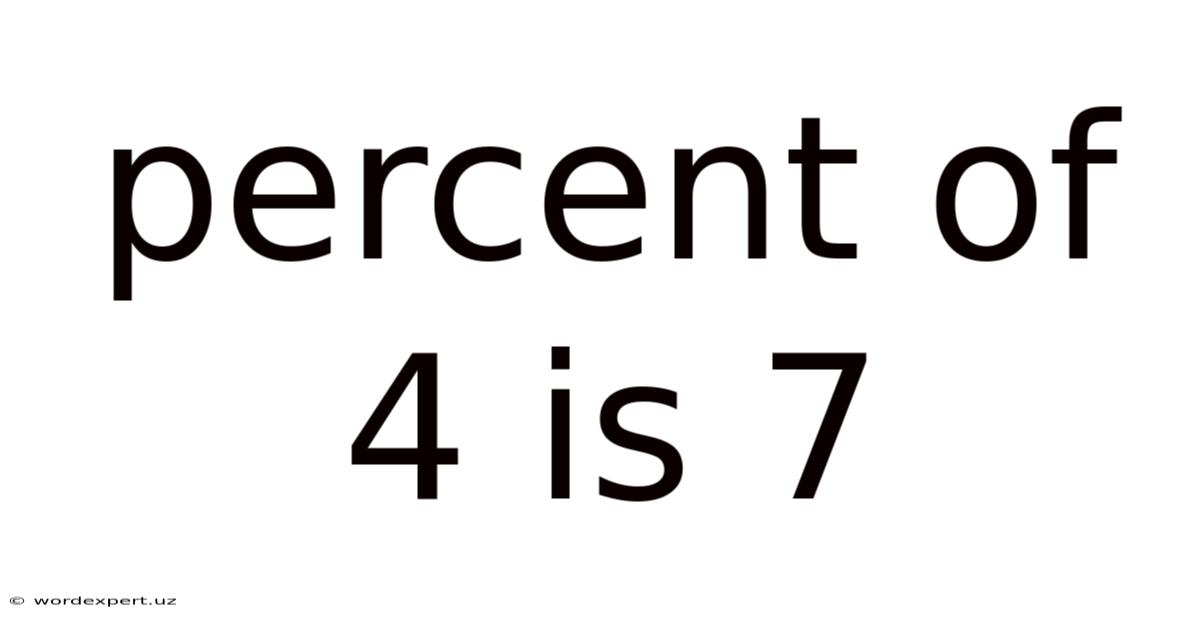
Table of Contents
Decoding the Paradox: Understanding "Percent of 4 is 7"
This seemingly simple statement, "percent of 4 is 7," presents a fascinating mathematical challenge. It's not a standard percentage problem because it reverses the typical setup. Instead of finding a percentage of a number, we're asked to find the percentage that results in a specific value when applied to 4. This article will delve into the solution, exploring different approaches, the underlying mathematical principles, and even extending the concept to broader applications. We'll uncover the logic behind this unique percentage problem and demonstrate how to solve similar puzzles. Understanding this seemingly contradictory statement allows us to grasp fundamental concepts of percentage calculations and problem-solving strategies.
Understanding the Problem: A Percentage Puzzle
The statement "percent of 4 is 7" is, at first glance, paradoxical. How can a percentage of a smaller number result in a larger number? This is where the crucial understanding of the problem's setup comes in. We're not looking for a percentage that's less than 100%. Instead, we're dealing with a percentage greater than 100%, meaning the resulting number will be larger than the original. This is a common misconception when dealing with percentage problems, and understanding this nuance is critical to finding the correct solution.
Method 1: Setting up the Equation
Let's represent the unknown percentage as 'x'. We can translate the statement "percent of 4 is 7" into a mathematical equation:
(x/100) * 4 = 7
This equation directly reflects the problem statement. 'x/100' represents the percentage as a decimal, multiplied by 4 (the base number) to equal 7 (the result). Now we can solve for 'x':
- Divide both sides by 4: (x/100) = 7/4 = 1.75
- Multiply both sides by 100: x = 1.75 * 100 = 175
Therefore, 175% of 4 is 7.
Method 2: Using Proportions
We can also approach this problem using proportions. We can set up a proportion where we compare the percentage to 100% and the resulting value (7) to the base value (4):
x/100 = 7/4
Cross-multiplying, we get:
4x = 700
Dividing both sides by 4:
x = 175
This method confirms our previous result: 175% of 4 is 7.
Method 3: Intuitive Understanding
While the algebraic methods are precise, it's helpful to develop an intuitive understanding. If 100% of 4 is 4, then to get to 7, we need to increase 4 by a certain percentage. The difference between 7 and 4 is 3. So we need to find what percentage of 4 equals 3.
This leads us to another equation:
(y/100) * 4 = 3
Solving for 'y':
y = (3/4) * 100 = 75
This means 75% of 4 is 3. Since we started with 4 (100% of 4) and added 3 (75% of 4) to reach 7, the total percentage is 100% + 75% = 175%.
This method underscores the importance of understanding the relationship between percentages, their decimal equivalents, and their practical application in problem-solving. It highlights the flexibility of percentage calculations and how different approaches can lead to the same solution.
The Concept of Percentages Greater Than 100%
This problem beautifully illustrates the concept of percentages exceeding 100%. Percentages are not limited to values between 0% and 100%. A percentage greater than 100% simply indicates an increase beyond the original value. For instance, a 150% increase means the value has increased by 50% of its original amount. In our example, a 175% of 4 means it has increased by 75% of 4 (which is 3).
Applying the Concept to Real-World Scenarios
The ability to solve problems involving percentages greater than 100% is essential in various real-world applications:
- Finance: Calculating returns on investments, inflation rates, or growth percentages. A 200% return on investment means your initial investment doubled.
- Business: Analyzing sales growth, profit margins, or market share changes. A 110% increase in sales means sales have increased by 10% compared to the previous period.
- Science: Expressing changes in population size, chemical concentrations, or experimental measurements.
- Data Analysis: Interpreting data trends and making predictions based on percentage changes.
Frequently Asked Questions (FAQ)
Q1: Why is this problem considered a "paradox"?
A1: The initial perception of a paradox stems from the unconventional nature of the problem. We're accustomed to finding a percentage of a number, resulting in a smaller or equal value. This problem reverses that, leading to a result larger than the base number. This unexpected result initially seems counterintuitive.
Q2: Can this method be used with other numbers?
A2: Absolutely! The same principles can be applied to similar problems. For example, to find the percentage of 6 that equals 9, you would set up the equation: (x/100) * 6 = 9, and solve for x, obtaining 150%.
Q3: What if the resulting number is smaller than the base number?
A3: In that case, the resulting percentage will be less than 100%. For example, if the problem was "percent of 10 is 5," the solution would be 50%.
Q4: Are there any limitations to this method?
A4: The method works consistently as long as the base number is not zero. Division by zero is undefined in mathematics, so this method cannot be applied if the base number is zero.
Conclusion: Mastering Percentage Calculations
The seemingly simple statement "percent of 4 is 7" presents a valuable opportunity to deepen our understanding of percentage calculations. By exploring various methods – algebraic equations, proportions, and intuitive reasoning – we've not only solved the problem but also reinforced fundamental mathematical principles. The ability to confidently tackle problems involving percentages greater than 100% is crucial for various applications, ranging from financial analysis to scientific data interpretation. This exercise showcases the versatility of percentage calculations and encourages a more nuanced approach to problem-solving. Remember that understanding the underlying principles, rather than simply memorizing formulas, is key to mastering any mathematical concept. This problem serves as a testament to the power of breaking down complex problems into manageable steps and applying logical reasoning to achieve a clear and accurate solution. This conceptual understanding will serve you well in tackling more complex mathematical scenarios and real-world applications.
Latest Posts
Latest Posts
-
60 Days From May 24
Sep 22, 2025
-
60 Days From July 30
Sep 22, 2025
-
86 Sq Meters To Feet
Sep 22, 2025
-
How Many Hours Till 9
Sep 22, 2025
-
How Many Ml Is 250mg
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Percent Of 4 Is 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.