Pv Of Growing Annuity Formula
wordexpert
Sep 22, 2025 · 6 min read
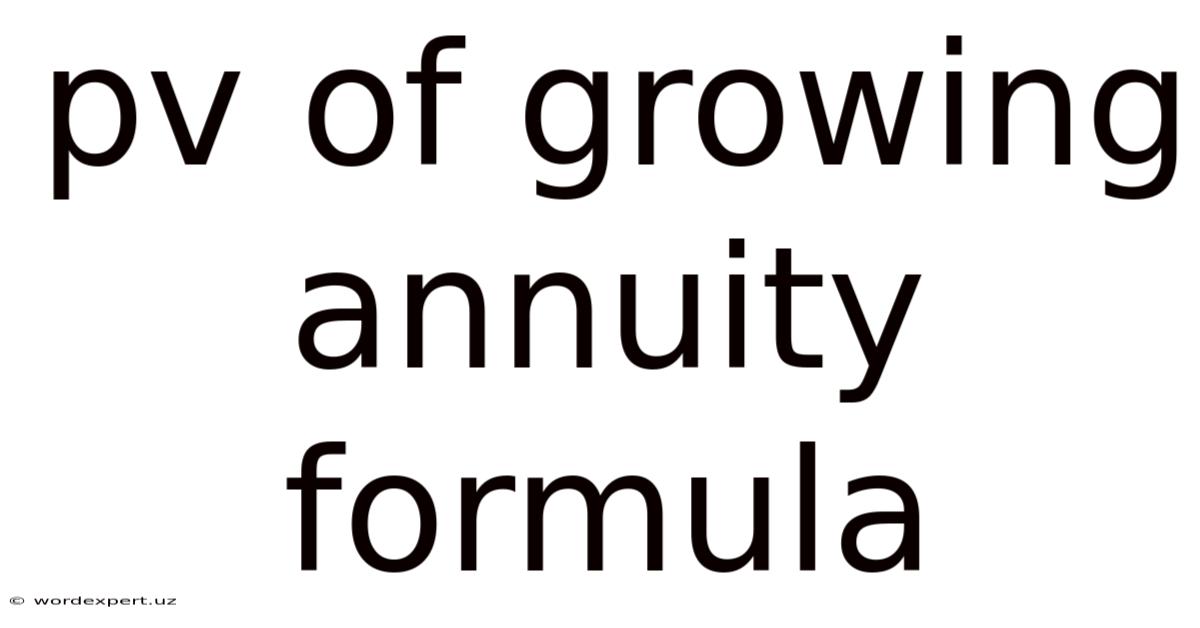
Table of Contents
Understanding the Present Value of a Growing Annuity: A Comprehensive Guide
The present value (PV) of a growing annuity is a crucial concept in finance, particularly in areas like investment analysis, retirement planning, and business valuation. It calculates the current worth of a series of future payments that increase at a constant rate over time. Unlike a regular annuity where payments remain the same, a growing annuity accounts for the impact of inflation, investment growth, or salary increases on future cash flows. This article provides a comprehensive understanding of the PV of a growing annuity formula, its applications, and the nuances involved in its calculation.
What is a Growing Annuity?
A growing annuity represents a stream of cash flows received at regular intervals, where each subsequent payment is larger than the preceding one by a fixed percentage. This percentage increase is known as the growth rate. Imagine receiving annual dividends from a stock that increases its payout each year, or receiving escalating rental income from a property. These scenarios exemplify growing annuities. Understanding their present value is critical for evaluating the overall worth of such investments.
The Formula for Present Value of a Growing Annuity
The formula for calculating the present value of a growing annuity is slightly more complex than that of a regular annuity because it incorporates the growth rate. The formula is:
PV = P * [(1 - (1 + g)^n * (1 + r)^-n) / (r - g)]
Where:
- PV = Present Value of the growing annuity
- P = The first payment (or payment at time 1)
- g = The constant growth rate of the payments (expressed as a decimal)
- r = The discount rate (or required rate of return, also expressed as a decimal)
- n = The number of periods (e.g., years)
Step-by-Step Calculation of PV of a Growing Annuity
Let's break down the formula and illustrate its application with an example:
Scenario: Assume you are considering an investment that promises to pay $1,000 at the end of the first year, with payments growing at a rate of 5% per year for the next 10 years. Your required rate of return (discount rate) is 8%.
Step 1: Identify the variables:
- P = $1,000
- g = 0.05 (5% growth rate)
- r = 0.08 (8% discount rate)
- n = 10 (number of years)
Step 2: Plug the values into the formula:
PV = $1,000 * [(1 - (1 + 0.05)^10 * (1 + 0.08)^-10) / (0.08 - 0.05)]
Step 3: Calculate the intermediate values:
- (1 + 0.05)^10 ≈ 1.6289
- (1 + 0.08)^-10 ≈ 0.4632
Step 4: Substitute the intermediate values:
PV = $1,000 * [(1 - (1.6289 * 0.4632)) / (0.03)]
Step 5: Complete the calculation:
- (1.6289 * 0.4632) ≈ 0.7539
- (1 - 0.7539) ≈ 0.2461
- 0.2461 / 0.03 ≈ 8.2033
- PV = $1,000 * 8.2033 ≈ $8,203.30
Therefore, the present value of this growing annuity is approximately $8,203.30. This means that receiving this stream of growing payments is equivalent to receiving a lump sum of $8,203.30 today.
Understanding the Components of the Formula
Let's delve deeper into the meaning of each component within the formula:
-
P (First Payment): This is the starting point of the annuity. The formula calculates the present value of the entire stream of payments based on this initial amount.
-
g (Growth Rate): The growth rate significantly influences the present value. A higher growth rate leads to a higher present value because future payments are larger. It reflects the anticipated increase in cash flows over time.
-
r (Discount Rate): The discount rate reflects the opportunity cost of capital. It's the rate of return an investor could earn on an alternative investment with similar risk. A higher discount rate leads to a lower present value because future cash flows are discounted more heavily. It represents the time value of money – money today is worth more than money in the future due to its earning potential.
-
n (Number of Periods): The number of periods determines the length of the annuity. A longer annuity (larger 'n') will generally have a higher present value, assuming a positive growth rate.
Important Considerations and Limitations
While the formula provides a powerful tool for valuing growing annuities, it's crucial to consider these limitations:
-
Constant Growth Rate: The formula assumes a constant growth rate throughout the annuity's life. In reality, growth rates can fluctuate.
-
Constant Discount Rate: Similarly, the formula assumes a constant discount rate. Changes in market conditions or the risk profile of the investment can affect the appropriate discount rate over time.
-
Growth Rate vs. Discount Rate: The formula breaks down if the growth rate (g) is equal to or greater than the discount rate (r). This is because the denominator (r - g) becomes zero or negative, resulting in an undefined or unrealistic present value. This scenario implies an impossibly high growth rate relative to the risk-adjusted return.
-
Timing of Payments: The formula assumes payments occur at the end of each period (ordinary annuity). If payments are made at the beginning of each period (annuity due), an adjustment is required to the formula. For an annuity due, you would multiply the calculated present value by (1 + r).
Practical Applications of PV of a Growing Annuity
The PV of a growing annuity finds widespread application across various financial domains:
-
Valuing Stocks: Analyzing dividend growth stocks, where dividends are expected to increase over time.
-
Retirement Planning: Calculating the present value of future pension payments or retirement savings.
-
Business Valuation: Determining the present value of future cash flows from a business.
-
Capital Budgeting: Assessing the value of investment projects with expected increasing cash inflows.
-
Lease Valuation: Determining the present value of future lease payments, especially if the payments are indexed to inflation.
-
Real Estate Investment: Evaluating the present value of future rental income from a property, accounting for rental increases.
Frequently Asked Questions (FAQs)
Q: What happens if the growth rate (g) is greater than the discount rate (r)?
A: The formula becomes invalid. It suggests an unrealistic scenario where the growth rate outpaces the required rate of return indefinitely, leading to an infinitely large present value.
Q: How does inflation affect the PV of a growing annuity?
A: Inflation influences both the growth rate and the discount rate. If you expect inflation, you should incorporate an inflation premium into both 'g' and 'r' to reflect the impact on future cash flows and their present value.
Q: Can I use this formula for annuities with irregular payments?
A: No. This formula is specifically designed for annuities with constant growth rates and equally spaced payments. For irregular payments, a more complex approach, such as discounted cash flow (DCF) analysis, is necessary.
Q: What software can I use to calculate the PV of a growing annuity?
A: Spreadsheet software like Microsoft Excel or Google Sheets offers built-in functions (like PV or financial functions) that can handle these calculations efficiently. Financial calculators also have dedicated functions for this purpose.
Conclusion
The present value of a growing annuity is a powerful tool for evaluating investments and financial streams that are expected to grow over time. Understanding the formula, its limitations, and its application across various financial contexts is crucial for making informed decisions. By correctly applying the formula and considering its nuances, investors and financial professionals can gain a more accurate and comprehensive understanding of the true worth of such investments. Remember that while the formula provides a valuable framework, it's always advisable to consider other factors and seek professional advice when making significant financial decisions.
Latest Posts
Latest Posts
-
30 Days From July 8
Sep 22, 2025
-
How Long Is 51 Hours
Sep 22, 2025
-
How Much Is 75 Cups
Sep 22, 2025
-
Percent Of 4 Is 7
Sep 22, 2025
-
Convert 200 G To Ounces
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Pv Of Growing Annuity Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.