What Is 10 Of 80000
wordexpert
Sep 23, 2025 · 5 min read
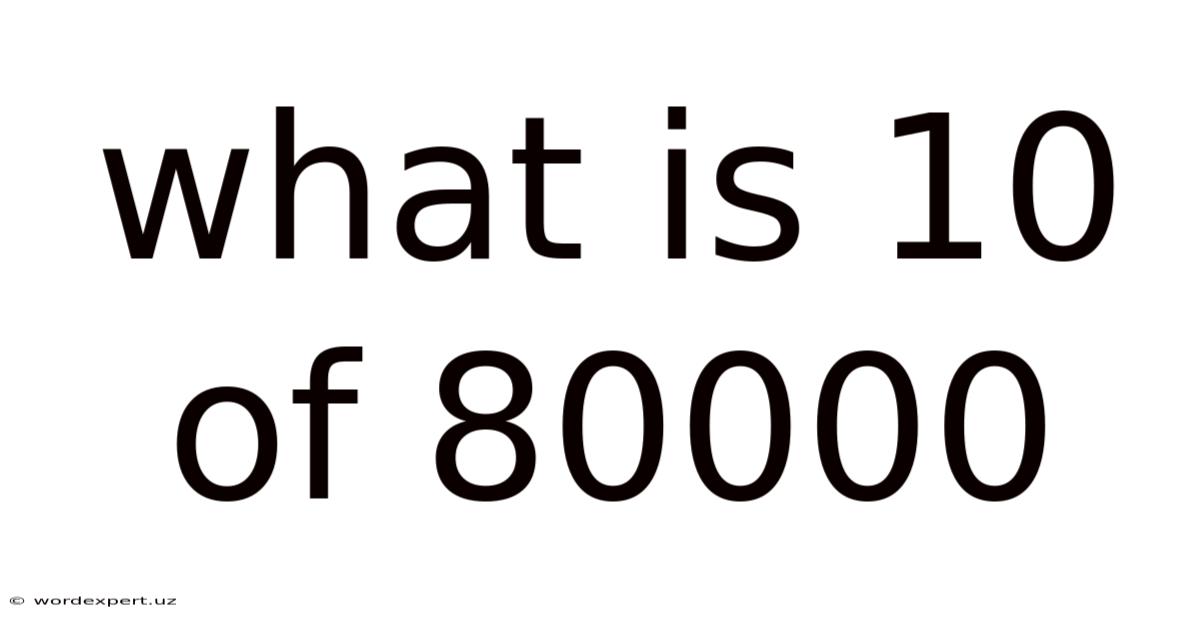
Table of Contents
What is 10% of 80,000? A Comprehensive Guide to Percentages and Their Applications
Finding 10% of 80,000 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various applications in everyday life, from budgeting and finance to understanding statistics and data analysis. This article will not only provide the answer but also delve into the methods used to calculate percentages, explore different approaches, and discuss the broader implications of percentage calculations.
Introduction: Understanding Percentages
Percentages are a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (Latin: per centum). They are used extensively to represent proportions, ratios, and changes in various contexts. For instance, we use percentages to describe discounts in shops (e.g., a 20% discount), interest rates on loans, exam scores, and much more. Understanding percentages is a fundamental skill in mathematics and crucial for navigating the quantitative aspects of modern life.
Calculating 10% of 80,000: The Simple Method
The most straightforward way to calculate 10% of 80,000 is to remember that 10% is equivalent to 1/10 (one-tenth). Therefore, finding 10% of a number simply involves dividing that number by 10.
In this case:
80,000 / 10 = 8,000
Therefore, 10% of 80,000 is 8,000.
Calculating Percentages: Alternative Methods
While the above method is the simplest for calculating 10%, other methods can be used for calculating different percentages. Let's explore some common approaches:
-
Method 1: Using Decimal Equivalents: Every percentage has a decimal equivalent. To convert a percentage to a decimal, simply divide the percentage by 100. For example, 10% becomes 0.10, 25% becomes 0.25, and so on. To find the percentage of a number, multiply the number by the decimal equivalent.
In our example:
80,000 x 0.10 = 8,000
-
Method 2: Using Fractions: Percentages can also be expressed as fractions. For instance, 10% is equivalent to 1/10, 25% is 1/4, 50% is 1/2, and so on. To find the percentage of a number, multiply the number by the equivalent fraction.
In our example:
80,000 x (1/10) = 8,000
-
Method 3: The Proportion Method: This method is particularly useful for solving more complex percentage problems. It involves setting up a proportion:
Part / Whole = Percentage / 100
To find 10% of 80,000, we would set up the proportion:
x / 80,000 = 10 / 100
Solving for x (cross-multiplying):
100x = 8,000,000
x = 8,000
Applications of Percentage Calculations in Real-Life Scenarios
Understanding percentage calculations is vital in various aspects of life. Here are some examples:
-
Finance: Calculating interest on loans, savings accounts, and investments. Understanding percentage changes in stock prices, analyzing financial statements, and budgeting all involve percentage calculations. For example, determining the amount of tax payable on income requires calculating a percentage of the total earnings.
-
Shopping: Calculating discounts, sales tax, and tips in restaurants. Understanding percentage markups by retailers is also essential for savvy consumers.
-
Statistics and Data Analysis: Percentages are essential for interpreting data, representing proportions within a dataset, and making comparisons. For example, the percentage of a population that supports a certain political candidate or the percentage of students who passed a specific exam are all calculated using percentage methods.
-
Science and Engineering: Percentages are used in various scientific calculations, such as calculating concentrations of solutions, expressing efficiencies of processes, and analyzing experimental data.
-
Everyday Life: Estimating percentages helps in everyday decision-making, such as calculating the tip amount in a restaurant or determining the portion sizes for recipes.
Beyond the Basics: More Complex Percentage Problems
While calculating 10% of 80,000 is relatively straightforward, percentage problems can become more complex. Here are some examples:
-
Finding the percentage increase or decrease: Suppose a value increases from 50,000 to 60,000. The percentage increase is calculated as: [(60,000 - 50,000) / 50,000] x 100 = 20%.
-
Finding the original value after a percentage change: If a value is decreased by 20% to 60,000, the original value can be found by solving the equation: x - (20/100)x = 60,000. This simplifies to 0.8x = 60,000, resulting in x = 75,000.
-
Calculating compound interest: This involves calculating interest not only on the principal amount but also on the accumulated interest from previous periods.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate percentages?
A: The easiest way depends on the specific percentage. For 10%, simply dividing by 10 is quickest. For other percentages, using the decimal equivalent is generally efficient.
-
Q: How can I improve my percentage calculation skills?
A: Practice is key. Work through various problems, starting with simple ones and gradually increasing the complexity. Use different methods to solve the same problem to understand their strengths and weaknesses.
-
Q: Are there any online tools or calculators that can help?
A: Yes, many online calculators are available that can perform percentage calculations quickly and accurately.
-
Q: Why are percentages important?
A: Percentages provide a standardized way to compare proportions, making it easier to understand data, make decisions, and communicate information effectively. They are essential for various applications in numerous fields.
-
Q: Can I use a calculator to solve percentage problems?
A: Absolutely! Calculators can simplify complex percentage calculations, especially those involving larger numbers or more intricate formulas. However, understanding the underlying principles is crucial for interpreting the results and solving problems effectively.
Conclusion: Mastering Percentage Calculations
Calculating 10% of 80,000, as we've seen, is a simple process yielding an answer of 8,000. However, this seemingly straightforward calculation highlights the broader importance of understanding percentages. From managing personal finances to interpreting complex datasets, a firm grasp of percentage calculations is a valuable skill applicable in numerous contexts. By mastering the different methods and understanding the underlying principles, you'll be well-equipped to tackle various percentage-related problems and navigate the quantitative aspects of life with greater confidence. Remember to practice regularly and explore different problem-solving approaches to build a strong foundation in this crucial mathematical concept.
Latest Posts
Latest Posts
-
Discharge Coefficient Vs Loss Coefficient
Sep 23, 2025
-
Gcf Of 36 And 81
Sep 23, 2025
-
600 Grams Flour To Cups
Sep 23, 2025
-
Dog Weight Predictor By Breed
Sep 23, 2025
-
1 Cup Rice Cooked Grams
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 80000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.