What Is 15 Of 80000
wordexpert
Sep 22, 2025 · 5 min read
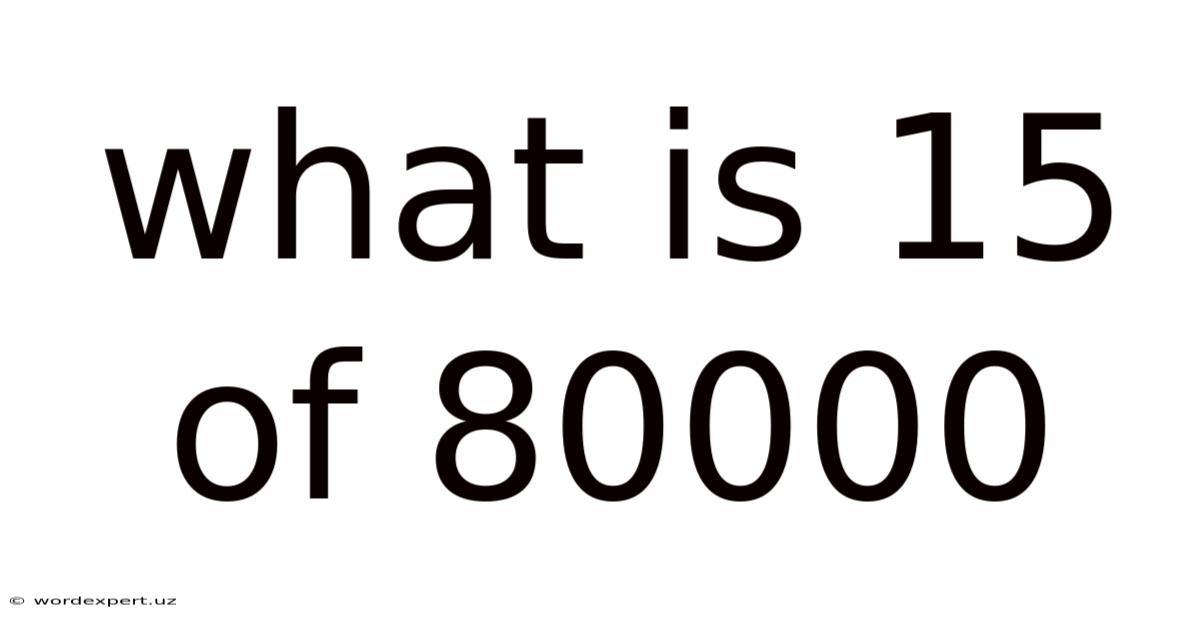
Table of Contents
What is 15% of 80,000? A Comprehensive Guide to Percentages and Calculations
Finding 15% of 80,000 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages and mastering different calculation methods can be incredibly useful in various aspects of life, from budgeting and financial planning to understanding statistical data and even baking! This comprehensive guide will not only solve this specific problem but also equip you with the knowledge and skills to tackle similar percentage calculations with confidence.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." So, 15% means 15 out of 100, or 15/100, which is equivalent to the decimal 0.15. Understanding this fundamental concept is crucial for tackling percentage problems.
Method 1: Using Decimal Multiplication
This is arguably the most straightforward method for calculating percentages. It involves converting the percentage into its decimal equivalent and then multiplying it by the number.
Steps:
-
Convert the percentage to a decimal: To convert 15% to a decimal, divide it by 100: 15 ÷ 100 = 0.15
-
Multiply the decimal by the number: Multiply 0.15 by 80,000: 0.15 x 80,000 = 12,000
Therefore, 15% of 80,000 is 12,000.
Method 2: Using Fraction Multiplication
This method involves converting the percentage into a fraction and then multiplying it by the number. This method is particularly useful when dealing with percentages that are easily expressed as simple fractions.
Steps:
-
Convert the percentage to a fraction: 15% can be written as 15/100. This fraction can be simplified by dividing both the numerator and the denominator by 5: 15/100 = 3/20
-
Multiply the fraction by the number: Multiply 3/20 by 80,000: (3/20) x 80,000 = 3 x (80,000/20) = 3 x 4,000 = 12,000
Therefore, 15% of 80,000 is 12,000.
Method 3: Using Proportions
This method uses the concept of ratios and proportions to solve the percentage problem. It's a more formal approach, often used in mathematical contexts.
Steps:
-
Set up a proportion: We can set up a proportion: 15/100 = x/80,000, where 'x' represents the unknown value (15% of 80,000).
-
Cross-multiply: Cross-multiplying gives us: 100x = 15 * 80,000
-
Solve for x: 100x = 1,200,000. Dividing both sides by 100 gives us: x = 12,000
Therefore, 15% of 80,000 is 12,000.
Real-World Applications: Why Understanding Percentages Matters
Understanding percentages is crucial for numerous real-world applications. Here are just a few examples:
-
Financial Calculations: Calculating taxes, interest rates, discounts, tips, and profit margins all rely heavily on percentage calculations. For instance, if a bank offers a 5% interest rate on a savings account, knowing how to calculate that percentage is essential to understanding your potential earnings. Similarly, understanding sales tax percentages helps you budget accurately for purchases.
-
Data Analysis: Percentages are fundamental to interpreting statistical data. Understanding percentage changes, growth rates, and market shares requires a strong grasp of percentage calculations. For example, analyzing sales figures often involves comparing percentage increases or decreases year-over-year.
-
Scientific Research: Many scientific experiments and studies involve expressing results as percentages. This is crucial for drawing meaningful conclusions from data.
-
Everyday Life: From calculating discounts at the store to understanding nutritional information on food labels (e.g., the percentage of daily value for certain nutrients), percentages are everywhere in our daily lives.
Beyond the Basics: More Complex Percentage Calculations
While the calculation of 15% of 80,000 is relatively straightforward, many real-world scenarios involve more complex percentage problems. Here are some examples:
-
Calculating the original price after a percentage discount: If an item is discounted by 20% and costs $60, you would need to use a different approach to find the original price.
-
Calculating percentage increase or decrease: Understanding how to calculate percentage changes is vital for analyzing trends and growth. For instance, calculating the percentage increase in population or sales figures requires a different formula.
-
Compound interest calculations: Compound interest involves calculating interest on both the principal amount and accumulated interest. This requires more advanced formulas.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method is often decimal multiplication. Simply convert the percentage to a decimal (by dividing by 100) and multiply it by the number.
Q: How can I improve my skills in calculating percentages?
A: Practice is key! Try working through different percentage problems, using different methods to reinforce your understanding. You can find plenty of practice problems online or in textbooks. Start with simple problems and gradually move to more complex ones.
Q: Are there any online calculators or tools that can help me with percentage calculations?
A: Yes, many online calculators and tools are available to help with percentage calculations. These can be particularly useful for more complex problems. However, understanding the underlying principles remains crucial.
Q: What if I need to calculate a percentage of a percentage?
A: Calculating a percentage of a percentage involves multiplying the percentages together (after converting them to decimals). For example, finding 10% of 20% is equivalent to 0.10 x 0.20 = 0.02, or 2%.
Conclusion: Mastering the Art of Percentages
Calculating 15% of 80,000, as we've demonstrated, is 12,000. However, the true value of this exercise lies in understanding the broader concept of percentages and the various methods for calculating them. This knowledge is a valuable tool applicable across various fields and essential for navigating everyday life and making informed decisions. By mastering these techniques, you'll be equipped to confidently tackle a wide range of percentage problems, from simple calculations to more complex scenarios involving financial planning, data analysis, and other applications. Remember to practice regularly and explore different calculation methods to build your skills and confidence.
Latest Posts
Latest Posts
-
Find The Indicated Z Score
Sep 22, 2025
-
90 Days From July 2
Sep 22, 2025
-
What Is A 55 Grade
Sep 22, 2025
-
Installing 100 Amp Sub Panel
Sep 22, 2025
-
Grams In A Quarter Ounce
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 80000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.