What Is 20 Off 35
wordexpert
Sep 21, 2025 · 4 min read
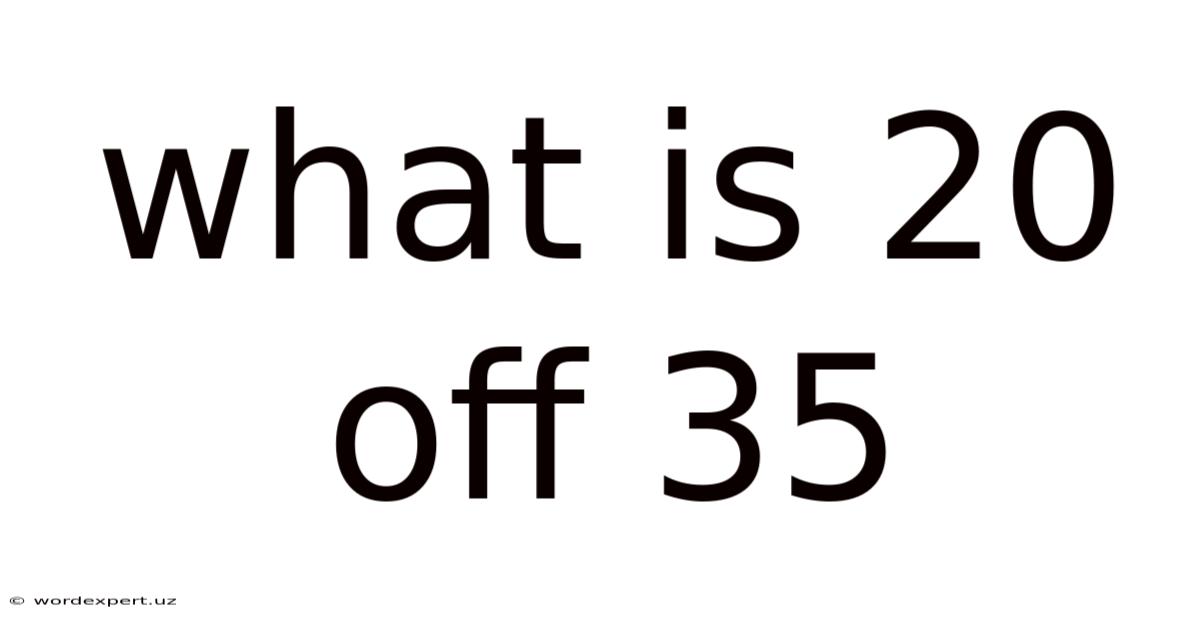
Table of Contents
What is 20% Off 35? A Comprehensive Guide to Percentage Discounts
Calculating discounts is a crucial life skill, applicable from everyday shopping to more complex financial scenarios. This article will delve into the seemingly simple question, "What is 20% off 35?", providing a thorough explanation, multiple methods for solving the problem, and exploring the broader context of percentage calculations. This guide aims to equip you with the knowledge and confidence to tackle similar percentage discount problems independently. Understanding percentage discounts is essential for budgeting, making informed purchasing decisions, and even understanding financial reports.
Understanding Percentage Discounts
Before jumping into the calculation, let's clarify the core concept. A percentage discount represents a reduction in the original price of an item. The percentage signifies the proportion of the original price that is being subtracted. In our case, "20% off 35" means we need to find 20% of 35 and then subtract that amount from 35 to find the final price.
Method 1: Calculating 20% of 35 Directly
The most straightforward method involves calculating 20% of 35 directly and then subtracting the result from the original price.
-
Convert the percentage to a decimal: To do this, divide the percentage by 100. So, 20% becomes 20/100 = 0.20.
-
Multiply the decimal by the original price: Multiply 0.20 by 35: 0.20 * 35 = 7. This represents the amount of the discount.
-
Subtract the discount from the original price: Subtract the discount (7) from the original price (35): 35 - 7 = 28.
Therefore, 20% off 35 is $\boxed{28}$.
Method 2: Calculating the Remaining Percentage
This method focuses on finding the percentage of the original price that remains after the discount.
-
Find the remaining percentage: If 20% is discounted, then 100% - 20% = 80% of the original price remains.
-
Convert the remaining percentage to a decimal: 80% becomes 80/100 = 0.80.
-
Multiply the decimal by the original price: Multiply 0.80 by 35: 0.80 * 35 = 28.
This directly gives us the final price after the discount, which is $\boxed{28}$.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the discounted price.
We can set up a proportion:
Let x be the discounted price.
20/100 = x/35
Cross-multiplying, we get:
100x = 20 * 35
100x = 700
x = 700/100
x = 7
This gives us the discount amount. To find the final price, subtract the discount from the original price: 35 - 7 = $\boxed{28}$
Understanding the Mathematical Principles
These methods all rely on fundamental mathematical principles:
-
Percentages: Percentages represent parts of a whole (100%). They are ratios expressed as fractions of 100.
-
Decimals: Decimals are another way of representing fractions, making them useful for calculations. Converting percentages to decimals simplifies multiplication.
-
Proportions: Proportions show the equality of two ratios. They are a powerful tool for solving problems involving relationships between different quantities.
Practical Applications and Real-World Examples
Understanding percentage discounts is crucial in numerous real-life scenarios:
-
Shopping: Calculating discounts on clothing, electronics, and other goods.
-
Sales Tax: Determining the final price after adding sales tax to a discounted item.
-
Investment Returns: Calculating the percentage increase or decrease in investment value.
-
Tips and Gratuities: Calculating tips based on a percentage of a meal cost.
-
Interest Rates: Understanding the impact of interest rates on loans and savings accounts.
Expanding Your Knowledge: Dealing with More Complex Scenarios
While this article focuses on a single discount calculation, the principles extend to more complex situations:
-
Multiple Discounts: If an item has multiple discounts applied sequentially (e.g., 20% off, then an additional 10% off), you would calculate each discount step-by-step.
-
Sales Tax: Remember to add the sales tax to the discounted price to find the total cost.
-
Compound Interest: Understanding compound interest involves calculating interest on the principal amount plus accumulated interest.
Frequently Asked Questions (FAQ)
Q: What if the discount is a different percentage?
A: You can use the same methods outlined above, simply replacing the 20% with the new percentage. Remember to convert the percentage to a decimal before multiplying by the original price.
Q: Can I use a calculator for these calculations?
A: Absolutely! Calculators are a valuable tool for these calculations, especially for larger numbers or more complex scenarios.
Q: Are there any online calculators available for percentage discounts?
A: Yes, many websites offer online calculators specifically designed for percentage discount calculations.
Conclusion: Mastering Percentage Discounts
Mastering percentage calculations is a valuable life skill with far-reaching applications. The seemingly simple question of "What is 20% off 35?" provides a foundation for understanding broader concepts in mathematics and finance. By understanding the different methods presented in this article and practicing regularly, you can confidently tackle similar percentage discount problems and make informed decisions in your daily life. Remember to break down complex problems into smaller, manageable steps, and don't hesitate to use calculators or online resources when needed. With practice and a solid understanding of the underlying principles, you'll become proficient in handling percentage discounts and a wide range of related calculations.
Latest Posts
Latest Posts
-
How Many Oz Is 3 4
Sep 21, 2025
-
Cuantas Onz Tiene Un Vaso
Sep 21, 2025
-
Cuantos Kilometros Son 19000 Pasos
Sep 21, 2025
-
How Long Is 700 Days
Sep 21, 2025
-
1 1 2 Pints To Cups
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Off 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.