What Is 40 Of 16
wordexpert
Sep 22, 2025 · 5 min read
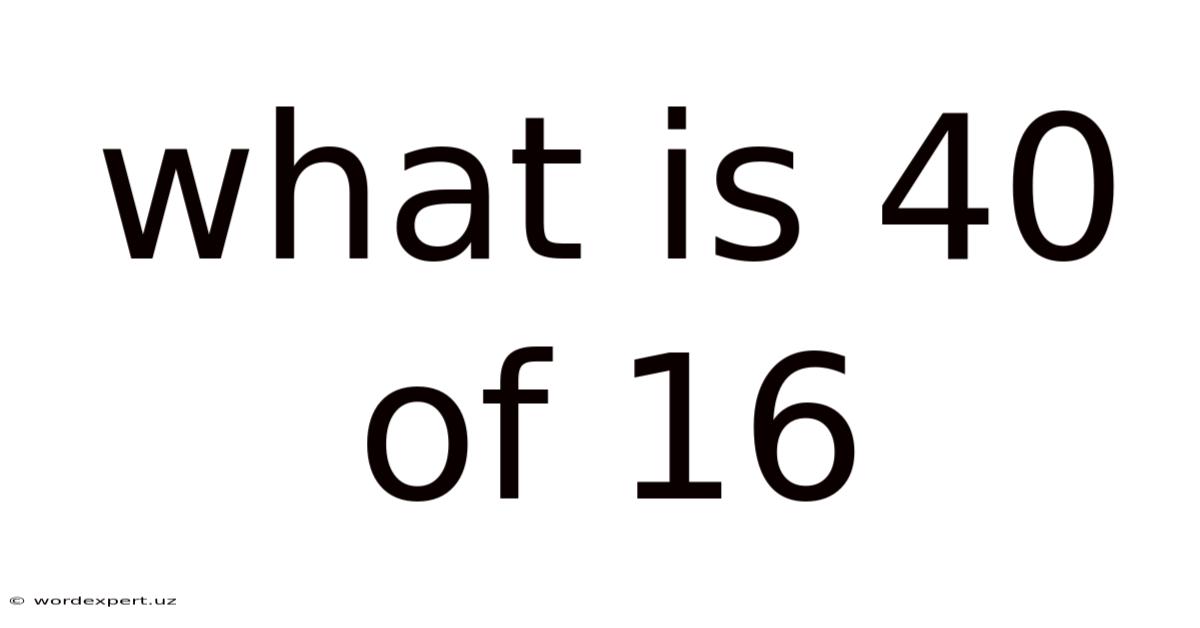
Table of Contents
What is 40% of 16? A Deep Dive into Percentages and Their Applications
Finding 40% of 16 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept in mathematics: percentages. This seemingly basic calculation has wide-ranging applications in everyday life, from calculating discounts in a store to understanding financial reports and even comprehending scientific data. This article will not only show you how to calculate 40% of 16 but also explore the underlying principles of percentages, different calculation methods, and real-world examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a fraction expressed as a number out of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 40% means 40 out of 100, or 40/100. This fraction can be simplified to 2/5. Understanding this fundamental concept is crucial for tackling percentage problems.
Method 1: Converting Percentage to a Decimal
This is arguably the most common and straightforward method. To find 40% of 16, we first convert the percentage into a decimal. We do this by dividing the percentage by 100:
40% ÷ 100 = 0.40 or simply 0.4
Now, we multiply this decimal by the number we want to find the percentage of:
0.4 * 16 = 6.4
Therefore, 40% of 16 is 6.4.
Method 2: Using Fractions
As mentioned earlier, 40% can be represented as the fraction 40/100, which simplifies to 2/5. We can use this fraction to calculate 40% of 16:
(2/5) * 16 = 32/5 = 6.4
This method offers a different perspective on the calculation and reinforces the connection between fractions and percentages.
Method 3: Proportions
This method is particularly useful for understanding the relationship between the percentage, the part, and the whole. We can set up a proportion:
40/100 = x/16
Where 'x' represents 40% of 16. To solve for x, we cross-multiply:
40 * 16 = 100 * x
640 = 100x
x = 640/100 = 6.4
Again, we find that 40% of 16 is 6.4. This method emphasizes the proportional relationship inherent in percentage calculations.
Real-World Applications: Where Percentages Matter
The ability to calculate percentages is essential in numerous real-life situations:
-
Shopping: Discounts are frequently expressed as percentages. If a $20 item is discounted by 40%, you can use the methods above to calculate the discount ($8) and the final price ($12).
-
Finance: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding percentages allows you to compare different financial products and make informed decisions. Calculating compound interest, a crucial concept in finance, heavily relies on percentage calculations.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of income or purchase price. Calculating these taxes accurately requires a solid understanding of percentages.
-
Statistics and Data Analysis: Percentages are used extensively in statistics to represent proportions and trends within data sets. For example, understanding the percentage of people who prefer a certain product or the percentage change in a stock price requires accurate percentage calculations.
-
Science: Percentages are used in various scientific fields to represent concentrations, yields, and changes in experimental results. For instance, calculating the percentage purity of a chemical compound or the percentage yield of a chemical reaction requires precise percentage calculations.
-
Everyday Life: Many everyday situations involve percentage calculations, such as calculating tips in restaurants, determining the percentage of completion of a task, or understanding the nutritional information on food labels.
Beyond the Basics: More Complex Percentage Problems
While finding 40% of 16 is a straightforward calculation, many real-world scenarios involve more complex problems. These might involve:
-
Finding the percentage increase or decrease: This involves calculating the percentage change between two values. For example, if the price of an item increases from $10 to $15, the percentage increase is calculated as follows: [(15-10)/10] * 100% = 50%.
-
Finding the original value after a percentage change: If an item is discounted by 20% and now costs $80, you can use algebraic equations to find the original price.
-
Calculating compound interest: This involves calculating interest not only on the principal amount but also on the accumulated interest.
-
Working with multiple percentages: This might involve applying several discounts or tax rates sequentially.
Frequently Asked Questions (FAQ)
-
Q: What are some common mistakes people make when calculating percentages?
- A: A common mistake is misinterpreting the meaning of percentage or incorrectly converting percentages to decimals. Another mistake is applying the percentage to the wrong value (e.g., applying a discount to the discounted price instead of the original price). Double-checking your work is essential to avoid such errors.
-
Q: Are there any online tools or calculators that can help with percentage calculations?
- A: Yes, many websites and apps offer percentage calculators that can handle various percentage-related problems. These calculators can be useful for double-checking your manual calculations or for solving more complex problems.
-
Q: How can I improve my understanding of percentages?
- A: Practice is key. Work through various percentage problems of increasing complexity. You can find practice problems in textbooks, online resources, or by creating real-world scenarios related to your own experiences. Understanding the fundamental concepts of fractions and decimals will also significantly improve your grasp of percentages.
Conclusion: Mastering the Power of Percentages
While the answer to "What is 40% of 16?" is a simple 6.4, the journey to finding this answer reveals the fundamental importance of understanding percentages. From everyday shopping to complex financial transactions and scientific analyses, the ability to calculate and interpret percentages is a crucial skill. By mastering the various methods outlined above and practicing regularly, you can confidently tackle a wide range of percentage problems and unlock their power in your personal and professional life. Remember, understanding percentages is not just about numbers; it's about understanding proportions, relationships, and changes in the world around us. So, embrace the challenge, and become proficient in this essential mathematical tool.
Latest Posts
Latest Posts
-
Convert Btu To Tons Calculator
Sep 22, 2025
-
Seconds In A N Hour
Sep 22, 2025
-
What Is 70 Of 400
Sep 22, 2025
-
Moment Of Inertia Calculator Beam
Sep 22, 2025
-
1 2 Cup Rice Calories Uncooked
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.