What Is 50 Of 16
wordexpert
Sep 18, 2025 · 5 min read
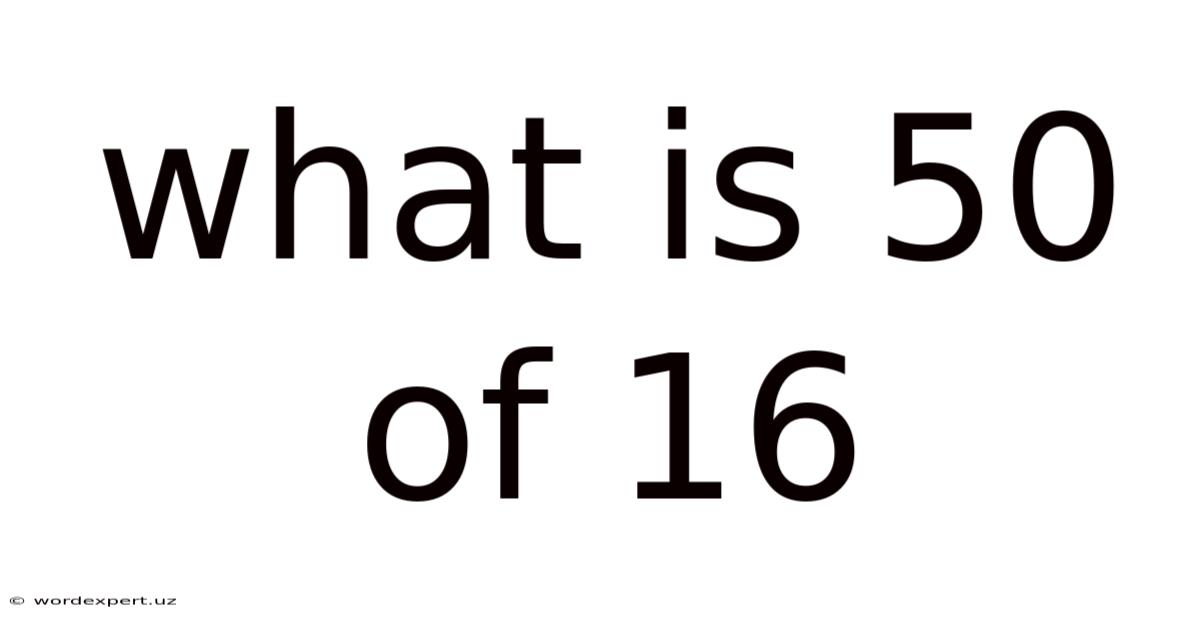
Table of Contents
Decoding 50% of 16: A Deep Dive into Percentages and Their Applications
Finding 50% of 16 might seem like a simple arithmetic problem, easily solvable with a quick calculation. However, understanding the underlying concept of percentages and their widespread applications goes far beyond this single calculation. This article delves into the meaning of percentages, provides multiple methods for calculating 50% of 16, explores the scientific basis of percentage calculations, and addresses frequently asked questions. By the end, you'll not only know the answer but also possess a deeper understanding of percentages and their importance in various fields.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per cent). Therefore, 50% signifies 50 parts out of 100 equal parts, which can be simplified to 1/2 or 0.5 as a decimal. Percentages are used extensively to represent proportions, ratios, and changes in various contexts, making them a fundamental concept in mathematics and beyond.
Method 1: The Direct Calculation Approach
The most straightforward method to find 50% of 16 is to directly apply the percentage definition. Since 50% represents half (50/100 = 1/2), finding 50% of 16 simply involves calculating half of 16.
16 / 2 = 8
Therefore, 50% of 16 is 8.
Method 2: Using Decimal Multiplication
Another common approach involves converting the percentage to a decimal and then multiplying it by the number. To convert 50% to a decimal, divide 50 by 100:
50 / 100 = 0.5
Now, multiply this decimal by 16:
0.5 * 16 = 8
This method confirms that 50% of 16 is indeed 8.
Method 3: Proportional Reasoning
This method is useful for understanding the underlying relationship between the percentage and the whole number. We can set up a proportion:
50/100 = x/16
Where 'x' represents the value we are trying to find (50% of 16). To solve for x, we cross-multiply:
50 * 16 = 100 * x
800 = 100x
x = 800 / 100
x = 8
Again, we arrive at the answer: 50% of 16 is 8.
The Mathematical Basis of Percentages
Percentage calculations are fundamentally based on the principles of fractions, decimals, and proportions. The core idea is to represent a part of a whole as a fraction of 100. This consistent base (100) allows for easy comparison and interpretation of proportions across different contexts.
-
Fractions: Percentages are directly related to fractions. For instance, 50% is equivalent to the fraction 50/100, which simplifies to 1/2. Converting percentages to fractions and vice versa is a crucial skill in understanding and manipulating percentages.
-
Decimals: Decimals provide another way to represent percentages. To convert a percentage to a decimal, divide the percentage by 100. For example, 50% becomes 0.5. Similarly, multiplying a decimal by 100 converts it back to a percentage.
-
Proportions: Proportions offer a powerful tool for solving percentage problems, particularly those involving finding an unknown part of a whole. Setting up a proportion allows us to use cross-multiplication to find the missing value.
Applications of Percentages in Real Life
The concept of percentages extends far beyond simple mathematical calculations. It plays a critical role in various aspects of daily life, including:
-
Finance: Interest rates, discounts, tax calculations, profit margins, and investment returns are all expressed as percentages. Understanding percentages is crucial for making informed financial decisions.
-
Science: Percentages are used to express concentrations of solutions, error margins in experiments, and statistical data analysis.
-
Statistics: Percentages are essential for presenting and interpreting data in surveys, polls, and research studies. They allow for easy comparison of different groups or categories.
-
Retail: Discounts, sales, and markups are commonly expressed as percentages, allowing consumers to quickly understand the price reductions or increases.
-
Healthcare: Percentages are used to describe the effectiveness of treatments, the prevalence of diseases, and the success rates of medical procedures.
Frequently Asked Questions (FAQ)
-
What if I need to find a different percentage of 16? The same methods can be applied. For example, to find 25% of 16, you would divide 16 by 4 (since 25% is 1/4) or multiply 16 by 0.25.
-
How do I calculate percentages with larger numbers? The same principles apply. Convert the percentage to a decimal and multiply it by the number. For example, to find 15% of 300, you would multiply 300 by 0.15.
-
What about percentages greater than 100%? These represent values exceeding the original whole. For instance, 150% of 16 would be 1.5 * 16 = 24. This indicates an increase of 50% over the original value.
-
Can I use a calculator for percentage calculations? Most calculators have a percentage function (%) that simplifies the process.
-
Are there online tools for calculating percentages? Yes, many websites and apps offer percentage calculators that can handle various percentage-related problems.
Conclusion: Beyond the Simple Calculation
While finding 50% of 16 yields a simple answer of 8, the true value lies in understanding the broader concept of percentages. Percentages are a fundamental tool in mathematics and are indispensable in countless real-world applications across various disciplines. Mastering percentage calculations not only enhances your mathematical abilities but also equips you with essential skills for navigating the numerical world around you. By grasping the underlying principles and utilizing different calculation methods, you can confidently tackle a wide range of percentage problems with precision and understanding. Remember, the journey of learning extends beyond a single answer; it’s about gaining a deeper understanding and applying that knowledge effectively.
Latest Posts
Latest Posts
-
When Is My Wedding Anniversary
Sep 18, 2025
-
Missouri State Auto Sales Tax
Sep 18, 2025
-
102 Cubic Inches To Ounces
Sep 18, 2025
-
What Is 18 20
Sep 18, 2025
-
Equation For Wet Bulb Temperature
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.