Whats 40 Percent Of 15
wordexpert
Sep 21, 2025 · 5 min read
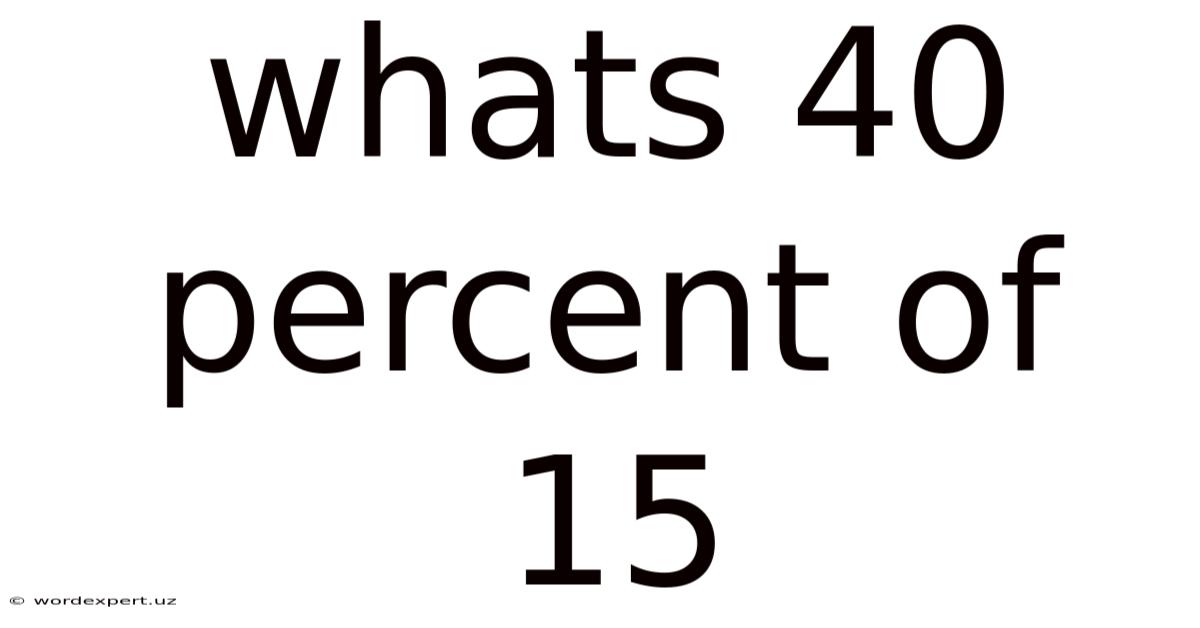
Table of Contents
What's 40 Percent of 15? A Deep Dive into Percentages and Their Applications
Finding 40 percent of 15 might seem like a simple calculation, a quick problem for a middle schooler. However, understanding how to solve this problem unlocks a world of practical applications in everyday life, from calculating discounts at the mall to understanding financial reports. This article will not only show you how to calculate 40% of 15 but also delve into the underlying concepts of percentages, explore different calculation methods, and highlight real-world examples where this fundamental skill becomes invaluable.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." When we say "40 percent," we mean 40 out of 100, or 40/100. This fraction can be simplified to 2/5. Understanding this fundamental concept is crucial to grasping percentage calculations.
Method 1: The Fraction Method – A Simple Approach
The most straightforward way to calculate 40% of 15 is by converting the percentage to a fraction and then multiplying.
-
Convert the percentage to a fraction: 40% is equivalent to 40/100, which simplifies to 2/5.
-
Multiply the fraction by the number: Multiply 2/5 by 15: (2/5) * 15 = 30/5
-
Simplify the fraction: 30/5 simplifies to 6.
Therefore, 40% of 15 is 6.
Method 2: The Decimal Method – Efficiency and Precision
Another common method involves converting the percentage to a decimal and then multiplying.
-
Convert the percentage to a decimal: To convert a percentage to a decimal, divide the percentage by 100. 40% divided by 100 is 0.40 or simply 0.4.
-
Multiply the decimal by the number: Multiply 0.4 by 15: 0.4 * 15 = 6
This method offers efficiency, especially when dealing with more complex percentage calculations. The result, once again, is 6.
Method 3: The Proportion Method – Understanding the Relationship
The proportion method provides a deeper understanding of the relationship between the percentage, the whole, and the part. We can set up a proportion:
40/100 = x/15
Where 'x' represents the unknown value (40% of 15). To solve for 'x', we cross-multiply:
40 * 15 = 100 * x
600 = 100x
x = 600/100
x = 6
This method reinforces the concept of proportionality and can be particularly helpful in solving more complex percentage problems.
Real-World Applications: Percentages in Daily Life
Understanding percentage calculations is crucial for navigating various aspects of daily life. Here are some examples:
-
Shopping Discounts: A common application is calculating discounts. If a store offers a 40% discount on a $15 item, you'd save $6 (40% of $15).
-
Sales Tax: Calculating sales tax involves finding a percentage of the original price. If the sales tax is 6%, you would calculate 6% of the purchase price to determine the total cost.
-
Tips and Gratuities: Restaurants often encourage tipping a certain percentage of the bill. Calculating a 20% tip on a $50 meal requires finding 20% of $50.
-
Financial Literacy: Understanding percentages is essential for interpreting financial statements, calculating interest rates on loans or savings accounts, and analyzing investment returns.
-
Grade Calculations: Many academic systems use percentages to represent grades, making it crucial to understand how your scores translate into percentages.
-
Data Analysis: Percentages are frequently used in data analysis to represent proportions and trends within datasets. Understanding these percentages allows for clearer interpretation of data and informed decision-making.
Beyond the Basics: Expanding Your Percentage Skills
While finding 40% of 15 is a fundamental exercise, mastering percentage calculations opens doors to solving more complex problems. Here are some extensions of this fundamental concept:
-
Finding the percentage: If you know the part and the whole, you can calculate the percentage. For example, if 6 is 40% of a number, what is the number? (This involves setting up a proportion or using algebraic equations.)
-
Finding the whole: If you know a percentage of a number and the value of that percentage, you can find the original number (the whole). This is often used in reverse percentage problems.
-
Compound percentages: These involve calculating percentages on top of previous percentages, often encountered in interest calculations. Understanding how compound interest works is essential for financial planning.
-
Percentage increase/decrease: Calculating the percentage change between two numbers is a crucial skill in various fields, from economics to science.
Frequently Asked Questions (FAQ)
-
What is the easiest way to calculate percentages? The decimal method is often the most efficient and straightforward, especially for those comfortable with decimal multiplication.
-
Can I use a calculator for percentage calculations? Absolutely! Most calculators have a percentage function (%) that simplifies the calculation process.
-
What if I need to calculate a percentage of a very large number? The decimal method remains efficient, even with large numbers. Calculators are highly recommended for accuracy.
-
Are there any online tools or resources available for percentage calculations? Numerous websites and apps provide percentage calculators and tutorials.
-
Why is understanding percentages important? Percentages are a fundamental aspect of numerical literacy, critical for everyday life, professional success, and informed decision-making.
Conclusion: Mastering the Power of Percentages
Understanding how to calculate 40% of 15, and more generally, mastering percentage calculations, is a valuable skill with widespread applications. It's not just about getting the right answer (which is 6); it's about understanding the underlying principles and their practical implications. By mastering these fundamental concepts, you equip yourself with a powerful tool for navigating the numerical world around you, making informed decisions, and achieving greater success in various aspects of life. The seemingly simple question, "What's 40 percent of 15?" opens the door to a deeper understanding of mathematics and its real-world applications. Remember that consistent practice and application are key to solidifying your understanding and improving your proficiency in percentage calculations.
Latest Posts
Latest Posts
-
Metric Conversion Chart To Inches
Sep 21, 2025
-
Is 6 A Perfect Square
Sep 21, 2025
-
What Is A 14 17 Grade
Sep 21, 2025
-
1 Million Days In Years
Sep 21, 2025
-
What Is A 14 18 Grade
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Whats 40 Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.