Whats 25 Percent Of 40
wordexpert
Sep 22, 2025 · 5 min read
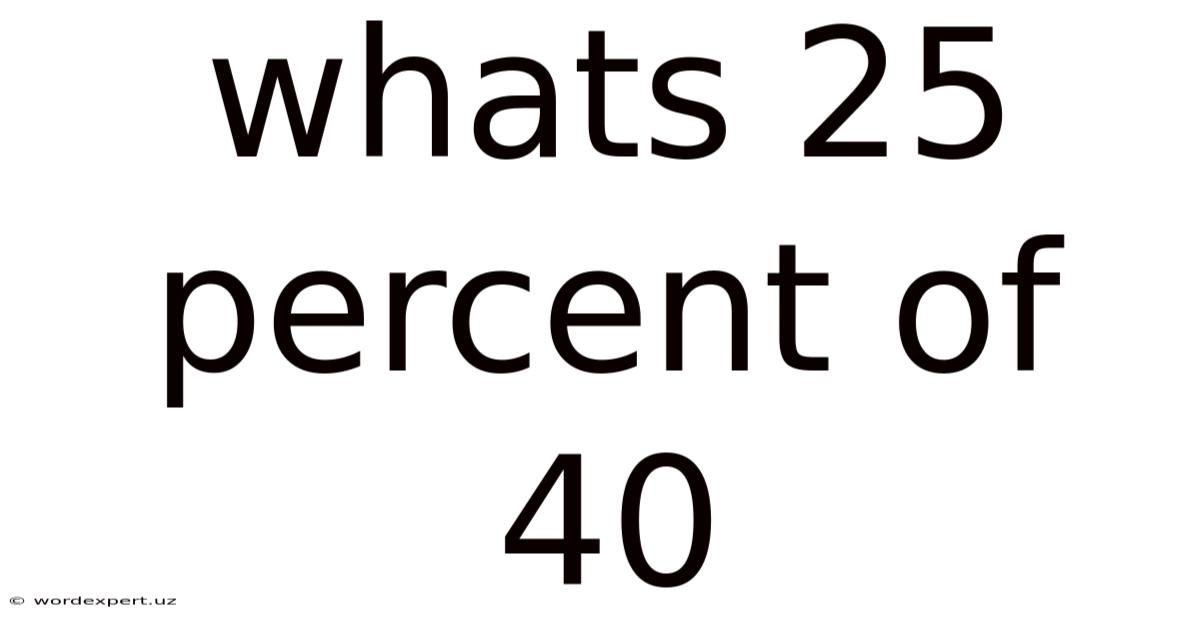
Table of Contents
What's 25 Percent of 40? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 40 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics: percentages. This seemingly basic question actually touches upon a wide range of applications, from everyday budgeting and shopping to complex financial calculations and scientific analyses. This article will not only answer the question directly but also explore the underlying principles, different methods for solving percentage problems, and the real-world significance of this seemingly simple calculation.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25. Understanding this foundational concept is crucial for tackling any percentage problem.
Method 1: Using the Fraction Method
The most straightforward way to calculate 25% of 40 is to convert the percentage to a fraction and then multiply.
-
Step 1: Convert the percentage to a fraction: 25% is equal to 25/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 25. This simplifies the fraction to 1/4.
-
Step 2: Multiply the fraction by the whole number: Now, multiply the simplified fraction (1/4) by 40: (1/4) * 40 = 10
Therefore, 25% of 40 is 10.
Method 2: Using the Decimal Method
Another common approach involves converting the percentage to a decimal before multiplying.
-
Step 1: Convert the percentage to a decimal: 25% is equal to 0.25 (simply divide 25 by 100).
-
Step 2: Multiply the decimal by the whole number: Multiply 0.25 by 40: 0.25 * 40 = 10
Again, we arrive at the answer: 25% of 40 is 10.
Method 3: Using Proportions
The concept of proportions offers a more visual and intuitive approach to solving percentage problems. A proportion sets up an equivalence between two ratios. We can set up a proportion as follows:
-
Let x represent the unknown value (25% of 40):
-
We can write the proportion: 25/100 = x/40
-
Cross-multiply: 25 * 40 = 100 * x
-
Solve for x: 1000 = 100x => x = 1000/100 = 10
Therefore, using proportions, we confirm that 25% of 40 is 10.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in various aspects of life:
-
Shopping and Sales: Calculating discounts during sales is a common application. For example, if a $40 item is on sale for 25% off, you would save $10 (25% of $40).
-
Finance and Budgeting: Percentages are fundamental in understanding interest rates, taxes, and investment returns. Calculating a 25% down payment on a house or figuring out the interest accrued on a loan requires a solid grasp of percentage calculations.
-
Data Analysis and Statistics: Percentages are used extensively in representing data in graphs and charts, making it easier to visualize and interpret trends and patterns. For example, representing the percentage of students who passed an exam or the percentage of market share held by a company.
-
Scientific Research: Percentages are used to express experimental results, error rates, and variations in data across multiple experiments.
-
Everyday Life: From calculating tips in restaurants to understanding nutritional information on food labels, percentages are constantly encountered in daily life.
Beyond the Basics: More Complex Percentage Problems
While finding 25% of 40 is relatively simple, percentage calculations can become more complex. Consider these scenarios:
-
Finding the Percentage: Instead of finding the percentage of a number, you might need to find what percentage one number is of another. For instance, what percentage of 40 is 10? (Answer: 25%)
-
Finding the Whole: You might know a percentage and its corresponding value, and need to find the original whole. For example, if 25% of a number is 10, what is the number? (Answer: 40)
-
Percentage Increase/Decrease: Calculating percentage increases or decreases involves finding the difference between two values and expressing that difference as a percentage of the original value.
Advanced Techniques: Using Formulas and Calculators
For more complex percentage problems, using formulas can streamline the process. The basic percentage formula is:
Percentage = (Part/Whole) * 100
Where:
- Part is the value you are considering as a percentage of the whole.
- Whole is the total value.
Scientific and financial calculators often have built-in functions for percentage calculations, making complex problems much easier to solve. However, understanding the underlying principles remains crucial, even when using these tools.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a different percentage of 40?
A: You can use the same methods described above, simply substituting the desired percentage for 25%. For example, to find 15% of 40, you would multiply 40 by 0.15 or 15/100.
-
Q: Are there any shortcuts for calculating common percentages?
A: Yes, memorizing some common percentage equivalents can speed up calculations. For example, 50% = 1/2, 25% = 1/4, 10% = 1/10, etc.
-
Q: What if I'm dealing with percentages greater than 100%?
A: Percentages greater than 100% represent values exceeding the whole. For example, 150% of 40 is 60 (1.5 * 40). This might represent an increase beyond the original value.
-
Q: How can I improve my understanding of percentages?
A: Practice is key! Solve various percentage problems using different methods. Start with simple examples and gradually work your way towards more complex calculations. Using online resources, workbooks, and educational materials can also enhance your understanding.
Conclusion: Mastering the Power of Percentages
While the seemingly simple question, "What's 25 percent of 40?" might appear trivial at first glance, it serves as a gateway to understanding a fundamental mathematical concept with wide-ranging applications. Through various methods—fractional, decimal, and proportional approaches—we’ve not only answered the question but also explored the underlying principles and diverse real-world applications of percentage calculations. By grasping these principles, you'll be well-equipped to tackle more complex percentage problems and confidently apply this essential skill in various academic, professional, and personal contexts. Remember, the key to mastering percentages lies in understanding the basic concepts and practicing regularly. The more you practice, the more intuitive and effortless these calculations will become.
Latest Posts
Latest Posts
-
30 Days From July 29
Sep 22, 2025
-
60 Days From August 15
Sep 22, 2025
-
90 Days From March 25
Sep 22, 2025
-
Aod 9604 How To Reconsitute
Sep 22, 2025
-
Kg Cm2 To Psia Conversion
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.